
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 1 | D. | 2 |
分析 对?x∈[0,+∞),不等式2ax≤ex-1恒成立,
等价于函数y=2ax的图象始终在函数y=ex-1图象的下方,其中x≥0;
在同一坐标系中画出函数y=2ax和y=ex-1的图象,结合图象求出a的最大值.
解答 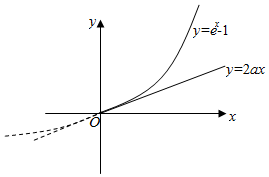 解:对?x∈[0,+∞),不等式2ax≤ex-1恒成立,
解:对?x∈[0,+∞),不等式2ax≤ex-1恒成立,
设y=2ax,y=ex-1,其中x≥0;
在同一坐标系中画出函数y=2ax和y=ex-1的图象如图所示;
则y′=ex,令x=0,得k=e0=1;
∴曲线y=ex-1过点O(0,0)的切线斜率为k=1;
根据题意得2a≤1,解得a≤$\frac{1}{2}$,
∴a的最大值为$\frac{1}{2}$.
故选:A.
点评 本题考查了不等式恒成立问题,解题时应用数形结合法,是中档题.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:解答题
 如图,有一边长为6的正方形铁片,在铁片的四角各截去一个边长为x的小正方形后,沿图中虚线部分折起,做成一个无盖方盒.
如图,有一边长为6的正方形铁片,在铁片的四角各截去一个边长为x的小正方形后,沿图中虚线部分折起,做成一个无盖方盒.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年 份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com