
���� ��1����D�������Բ�������a���ɣ�
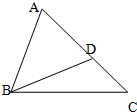
��2������GF1��DF1�����ı���DF1GF2��ƽ���ı��Σ�������Բ�Ķ���ó������ε��ܳ������������ʽ���������
��3����P��2cos�ȣ�sin�ȣ����������Ǻ�����ȱ任����kPD•kPG���ɵó����ۣ�
��� �⣺��1����D��$\frac{2}{3}$��$\frac{2\sqrt{2}}{3}$������ԲE�ϣ�
��$\frac{4}{9{a}^{2}}$+$\frac{8}{9}$=1�����a2=4��
����Բ�ķ���Ϊ��$\frac{{x}^{2}}{4}+{y}^{2}=1$��
��2���ߵ�GΪ��D����ԭ��ĶԳƵ㣬��G��-$\frac{2}{3}$��-$\frac{2\sqrt{2}}{3}$����
��F2��$\sqrt{3}$��0������DG=2OD=2$\sqrt{��\frac{2}{3}��^{2}+��\frac{2\sqrt{2}}{3}��^{2}}$=$\frac{4\sqrt{3}}{3}$��
����DF1��GF1�����ı���DF1GF2��ƽ���ı��Σ�
��DF2+GF2=DF2+DF1=2a=4��
���F2DG���ܳ�Ϊ4+$\frac{4\sqrt{3}}{3}$��
���F2DG�����Ϊ2S${\;}_{��OD{F}_{2}}$=2��$\frac{1}{2}$��OF2��yD=$\sqrt{3}��\frac{2\sqrt{2}}{3}$=$\frac{2\sqrt{6}}{3}$��
��3����P������Ϊ��2cos�ȣ�sin�ȣ�����kPD=$\frac{sin��-\frac{2\sqrt{2}}{3}}{2cos��-\frac{2}{3}}$=$\frac{3sin��-2\sqrt{2}}{6cos��-2}$��
kPG=$\frac{sin��+\frac{2\sqrt{2}}{3}}{2cos��+\frac{2}{3}}$=$\frac{3sin��+2\sqrt{2}}{6cos��+2}$��
��kPD•kPG=$\frac{3sin��-2\sqrt{2}}{6cos��-2}$•$\frac{3sin��+2\sqrt{2}}{6cos��+2}$=$\frac{9si{n}^{2}��-8}{36co{s}^{2}��-4}$=$\frac{1-9co{s}^{2}��}{36co{s}^{2}��-4}$=-$\frac{1}{4}$��
��ֱ��PD��PG��б�ʳ˻���ֵ-$\frac{1}{4}$��
���� ���⿼������Բ�����ʣ�ֱ������Բ��λ�ù�ϵ�������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a+b��c+d⇒a��c��b��d | B�� | ac2��bc2⇒a��b | ||
| C�� | $\frac{c}{a}$��$\frac{b}{d}$⇒ab��cd | D�� | $\sqrt{a}$��$\sqrt{b}$?a��b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8 | B�� | 10 | C�� | 12 | D�� | 14 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{6}}{6}$ | B�� | $\frac{\sqrt{3}}{6}$ | C�� | $\frac{\sqrt{30}}{6}$ | D�� | $\frac{\sqrt{6}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com