
【题目】已知曲线C1 , C2的极坐标方程分别为ρ=2cosθ, ![]() ,射线θ=φ,
,射线θ=φ, ![]() ,
, ![]() 与曲线C1交于(不包括极点O)三点A,B,C.
与曲线C1交于(不包括极点O)三点A,B,C.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)当 ![]() 时,求点B到曲线C2上的点的距离的最小值.
时,求点B到曲线C2上的点的距离的最小值.
【答案】解:(Ⅰ)依题意|OA|=2cosφ, ![]() ,
, ![]() ,
,
则 ![]()
![]()
=4cosφcos ![]()
= ![]()
=![]() .
.
(Ⅱ)解:∵ ![]() ,
,
∴ ![]() ,
,
曲线C2的直角坐标方程为 ![]() .
.
又∵B的极坐标为(1, ![]() ),化为直角坐标为(
),化为直角坐标为( ![]() ,
, ![]() ),
),
∴B到曲线C2的距离为 ![]() ,
,
∴所求距离的最小值为 ![]() .
.
【解析】(Ⅰ)先根据题用φ表示出OA,OB,OC的模长,经计算即可得出三者的关系;(Ⅱ)先求得曲线C2的直角坐标方程并可知其为直线,再将点B的极坐标化为直角坐标,从而根据点到直线的距离公式求得点B到曲线C2的距离的最小值.
【考点精析】掌握三角函数的积化和差公式和三角函数的和差化积公式是解答本题的根本,需要知道三角函数的积化和差公式:![]() ;
;![]() ;三角函数的和差化积公式:
;三角函数的和差化积公式:![]() =
=![]() (辅助角
(辅助角![]() 所在象限由点
所在象限由点![]() 的象限决定,
的象限决定,![]() ).
).


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的方程是
的方程是![]() .
.
(![]() )如果圆
)如果圆![]() 与直线
与直线![]() 没有公共点,求实数
没有公共点,求实数![]() 的取值范围;
的取值范围;
(![]() )如果圆
)如果圆![]() 过坐标原点,过点
过坐标原点,过点![]() 直线
直线![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点,记直线
两点,记直线![]() 的斜率的平方为
的斜率的平方为![]() ,对于每一个确定的
,对于每一个确定的![]() ,当
,当![]() 的面积最大时,用含
的面积最大时,用含![]() 的代数式表示
的代数式表示![]() ,并求
,并求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}中,定义:dn=an+2+an﹣2an+1(n≥1),a1=1.
(1)若dn=an , a2=2,求an;
(2)若a2=﹣2,dn≥1,求证此数列满足an≥﹣5(n∈N*);
(3)若|dn|=1,a2=1且数列{an}的周期为4,即an+4=an(n≥1),写出所有符合条件的{dn}.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形∠CAB=90°,AC=2a,E,F分别为AC,BC的中点,沿EF将△CEF折起,得到如图2所示的四棱锥C′﹣ABFE
(1)求证:AB⊥平面AEC′;
(2)当四棱锥C′﹣ABFE体积取最大值时,
①若G为BC′中点,求异面直线GF与AC′所成角;
②在C′﹣ABFE中AE交BF于C,求二面角A﹣CC′﹣B的余弦值.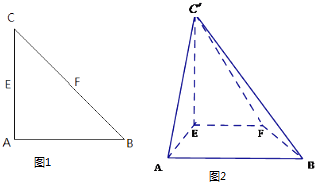
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是异面直线,则以下四个命题:①存在分别经过直线
是异面直线,则以下四个命题:①存在分别经过直线![]() 和
和![]() 的两个互相垂直的平面;②存在分别经过直线
的两个互相垂直的平面;②存在分别经过直线![]() 和
和![]() 的两个平行平面;③经过直线
的两个平行平面;③经过直线![]() 有且只有一个平面垂直于直线
有且只有一个平面垂直于直线![]() ;④经过直线
;④经过直线![]() 有且只有一个平面平行于直线
有且只有一个平面平行于直线![]() ,其中正确的个数有( )
,其中正确的个数有( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先阅读下列结论的证法,再解决后面的问题:
已知 ![]() ,求证:
,求证: ![]() .
.
【证明】构造函数 ![]() ,则
,则 ![]() ,
,
因为对一切 ![]() ,恒有
,恒有 ![]() .
.
所以 ![]() ,从而得
,从而得 ![]() .
.
(1)若 ![]() ,请写出上述结论的推广式;
,请写出上述结论的推广式;
(2)参考上述解法,对你推广的结论加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查喜欢旅游是否与性别有关,调查人员就“是否喜欢旅游”这个问题,在火车站分别随机调研了 ![]() 名女性或
名女性或 ![]() 名男性,根据调研结果得到如图所示的等高条形图.
名男性,根据调研结果得到如图所示的等高条形图.
(1)完成下列 ![]() 列联表:
列联表:
喜欢旅游 | 不喜欢旅游 | 估计 | |
女性 | |||
男性 | |||
合计 |
(2)能否在犯错误概率不超过 ![]() 的前提下认为“喜欢旅游与性别有关”.
的前提下认为“喜欢旅游与性别有关”.
附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:![]() ,其中
,其中 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来,引发各方关注,收视率、点击率均占据各大排行榜首位.我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查,共调查了600人,得到结果如下:其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图;表1是不同年龄段的观众选择不同观看方式的人数.
表1
观看方式 | 电视 | 网络 |
| 150 | 250 |
| 120 | 80 |
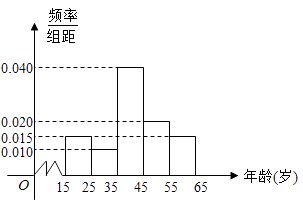
求:(I)假设同一组中的每个数据用该组区间的中点值代替,求非常喜欢《人民的名义》这部电视剧的观众的平均年龄;
(II)根据表1,通过计算说明我们是否有99%的把握认为观看该剧的方式与年龄有关?
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附: ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com