
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由已知列式求得b值,得到函数解析式,然后利用裂项相消法求出数列|$\frac{1}{f(n)}$|的前n项和为Sn,再由Sn>$\frac{5}{12}$变形整理得到满足Sn>$\frac{5}{12}$的最小正整数.
解答 解:f(x)=x2+bx,得f′(x)=2x+b,
则k=f′(2)=2×2+b=4+b=6,得b=2.
则f(x)=x2+2x,∴f(n)=n2+bn,
${a}_{n}=|\frac{1}{f(n)}|=\frac{1}{{n}^{2}+2n}=\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,
∴Sn=$\frac{1}{2}[(1-\frac{1}{3})+(\frac{1}{2}-\frac{1}{4})+…+(\frac{1}{n-1}-\frac{1}{n+1})+(\frac{1}{n}-\frac{1}{n+2})]$
=$\frac{1}{2}(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2})$=$\frac{3}{4}-\frac{2n+3}{2{n}^{2}+6n+4}$>$\frac{5}{12}$,
化简得:2n2-5>0.
满足这个不等式的最小正整数为2.
故选:B.
点评 本题考查利用导数研究过曲线上某点处的切线方程,考查了裂项相消法求数列的和,考查数列不等式的解法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | $({0,\sqrt{3}})$ | B. | $({0,1})∪({1,\sqrt{3}})$ | C. | $({1,\sqrt{3}})$ | D. | (0,1)∪(1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x0<a | B. | x0>b | C. | x0<c | D. | x0>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
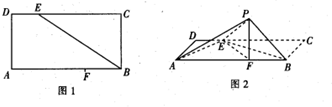 如图1,矩形ABCD中,AB=12,AD=6,E,F分别为CD,AB边上的点,且DE=3,BF=4,将△BCE沿BE折起至△PBE位置(如图2所示),连接AP、EF、PF,其中PF=2$\sqrt{5}$.
如图1,矩形ABCD中,AB=12,AD=6,E,F分别为CD,AB边上的点,且DE=3,BF=4,将△BCE沿BE折起至△PBE位置(如图2所示),连接AP、EF、PF,其中PF=2$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (40,64) | B. | [40,64] | C. | (-∞,40)∪(64,+∞) | D. | (-∞,40]∪[64,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com