
| A. | (-∞,3] | B. | (-2,$\frac{1}{2}$] | C. | [$\frac{1}{2}$,3] | D. | [$\frac{1}{2}$,+∞) |
分析 把已知函数解析式变形,可得f(x)=$\frac{3-2x}{x+1}$=$\frac{5}{x+1}-2$,利用函数单调性求得g(x)=$\frac{5}{x+1}$的范围得答案.
解答 解:f(x)=$\frac{3-2x}{x+1}$=$\frac{5}{x+1}-2$,
设g(x)=$\frac{5}{x+1}$,
∵g(x)在x∈[0,1]上单调递减,
∴$g(x)_{min}=g(1)=\frac{5}{2}$,g(x)max=g(0)=5.
∴函数f(x)=$\frac{3-2x}{x+1}$(x∈[0,1])的值域为:[$\frac{1}{2}$,3].
故选:C.
点评 本题考查利用函数的单调性求函数的值域,是基础的计算题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,平行四边形ABCD,点E、F分别是DC,BC的中点,$\overrightarrow{AC}$=$λ\overrightarrow{AE}$-$μ\overrightarrow{AF}$,则λ+μ=0.
如图,平行四边形ABCD,点E、F分别是DC,BC的中点,$\overrightarrow{AC}$=$λ\overrightarrow{AE}$-$μ\overrightarrow{AF}$,则λ+μ=0.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 以上都有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
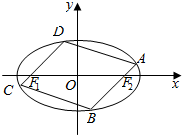 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴的一个顶点与两个焦点构成正三角形,且该三角形的面积为$\sqrt{3}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴的一个顶点与两个焦点构成正三角形,且该三角形的面积为$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com