练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】二次函数y=ax2+bx和反比例函数 在同一坐标系中的图象大致是（ ）
    A.
    B.
    C.
    D.

    【答案】B
    【解析】解：当a＞0时，b＞0时，二次函数二次函数y=ax2+bx图象开口向上，且对称轴x=﹣ ＜0，反比例函数 在第一，三象限且为减函数，故A不正确，
    当a＞0时，b＜0时，二次函数二次函数y=ax2+bx图象开口向上，且对称轴x=﹣ ＞0，反比例函数 在第二，四象限且为增函数，故D不正确，
    当a＜0时，b＞0时，二次函数二次函数y=ax2+bx图象开口向下，且对称轴x=﹣ ＞0，反比例函数 在第一，三象限且为减函数，故B正确，
    当a＜0时，b＜0时，二次函数二次函数y=ax2+bx图象开口向上，且对称轴x=﹣ ＜0，反比例函数 在第二，四象限且为增函数，故C不正确，
    故选：B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】给定映射f：（x，y）→（x+2y，2x﹣y），在映射f下（3，1）的原象为（ ）
    A.（1，3）
    B.（3，1）
    C.（1，1）
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校高一 、高二 、高三三个年级共有 名教师，为调查他们的备课时间情况，通过分层

    抽样获得了名教师一周的备课时间 ，数据如下表（单位 ：小时）：

    高一年级

    高二年级

    高三年级

    （1）试估计该校高三年级的教师人数 ；

    （2）从高一年级和高二年级抽出的教师中，各随机选取一人，高一年级选出的人记为甲 ，高二年级选出的人记为乙 ，求该周甲的备课时间不比乙的备课时间长的概率 ；

    （3）再从高一、高二、高三三个年级中各随机抽取一名教师，他们该周的备课时间分别是（单位： 小时），这三个数据与表格中的数据构成的新样本的平均数记为，表格中的数据平均数记为 ，试判断与的大小. （结论不要求证明）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

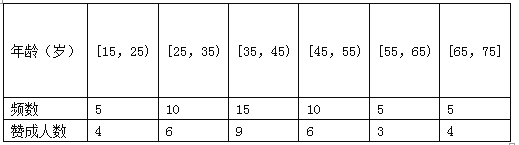
    【题目】私家车的尾气排放是造成雾霾天气的重要因素之一，因此在生活中我们应该提倡低碳生活，少开私家车，尽量选择绿色出行方式，为预防雾霾出一份力．为此，很多城市实施了机动车车尾号限行，我市某报社为了解市区公众对“车辆限行”的态度，随机抽查了50人，将调查情况进行整理后制成下表：

    （Ⅰ）完成被调查人员的频率分布直方图；

    （Ⅱ）若从年龄在[15，25），[25，35）的被调查者中各随机选取2人进行追踪调查，求恰有2人不赞成的概率；

    （Ⅲ）在（Ⅱ）的条件下，再记选中的4人中不赞成“车辆限行”的人数为，求随机变量的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆： 的上下顶点分别为，且点． 分别为椭圆的左、右焦点，且．

    （Ⅰ）求椭圆的标准方程；

    （Ⅱ）点是椭圆上异于， 的任意一点，过点作轴于， 为线段

    的中点．直线与直线交于点， 为线段的中点， 为坐标原点．求

    的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两名射手在一次射击中的得分是两个随机变量，分别记为X和Y，它们的分布列分别为

    X

    0

    1

    2

    P

    0.1

    a

    0.4

    Y

    0

    1

    2

    P

    0.2

    0.2

    b


    （1）求a，b的值；
    （2）计算X和Y的期望与方差，并以此分析甲、乙两射手的技术情况．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设，若存在常数，使得对任意，均有，则称为有界集合，同时称为集合的上界．

    （1）设、，试判断、是否为有界集合，并说明理由；

    （2）已知，记（）．若，

    ，且为有界集合，求的值及的取值范围；

    （3）设均为正数，将中的最小数记为．是否存在正数，使得为有界集合， 均为正数的上界，若存在，试求的最小值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数y=f（x），若在定义域内存在x0 ， 使得f（﹣x0）=﹣f（x0）成立，则称x0为函数y=f（x）的局部对称点．
    （1）若a、b∈R且a≠0，证明：函数f（x）=ax2+bx﹣a必有局部对称点；
    （2）若函数f（x）=2x+c在定义域[﹣1，2]内有局部对称点，求实数c的取值范围；
    （3）若函数f（x）=4x﹣m2x+1+m2﹣3在R上有局部对称点，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足Sn+an=2n+1．
    （1）写出a1 ， a2 ， a3 ， 并推测an的表达式；
    （2）用数学归纳法证明所得的结论．

    查看答案和解析>>

    同步练习册答案