
ЁОЬтФПЁПФГбЇаЃИпвЛ ЁЂИпЖў ЁЂИпШ§Ш§ИіФъМЖЙВга ![]() УћНЬЪІЃЌЮЊЕїВщЫћУЧЕФБИПЮЪБМфЧщПіЃЌЭЈЙ§ЗжВу
УћНЬЪІЃЌЮЊЕїВщЫћУЧЕФБИПЮЪБМфЧщПіЃЌЭЈЙ§ЗжВу
ГщбљЛёЕУСЫ![]() УћНЬЪІвЛжмЕФБИПЮЪБМф ЃЌЪ§ОнШчЯТБэЃЈЕЅЮЛ ЃКаЁЪБЃЉЃК
УћНЬЪІвЛжмЕФБИПЮЪБМф ЃЌЪ§ОнШчЯТБэЃЈЕЅЮЛ ЃКаЁЪБЃЉЃК
ИпвЛФъМЖ |
|
|
|
|
| |||
ИпЖўФъМЖ |
|
|
|
|
|
|
| |
ИпШ§ФъМЖ |
|
|
|
|
|
|
|
|
ЃЈ1ЃЉЪдЙРМЦИУаЃИпШ§ФъМЖЕФНЬЪІШЫЪ§ ЃЛ
ЃЈ2ЃЉДгИпвЛФъМЖКЭИпЖўФъМЖГщГіЕФНЬЪІжаЃЌИїЫцЛњбЁШЁвЛШЫЃЌИпвЛФъМЖбЁГіЕФШЫМЧЮЊМз ЃЌИпЖўФъМЖбЁГіЕФШЫМЧЮЊвв ЃЌЧѓИУжмМзЕФБИПЮЪБМфВЛБШввЕФБИПЮЪБМфГЄЕФИХТЪ ЃЛ
ЃЈ3ЃЉдйДгИпвЛЁЂИпЖўЁЂИпШ§Ш§ИіФъМЖжаИїЫцЛњГщШЁвЛУћНЬЪІЃЌЫћУЧИУжмЕФБИПЮЪБМфЗжБ№ЪЧ![]() ЃЈЕЅЮЛЃК аЁЪБЃЉЃЌетШ§ИіЪ§ОнгыБэИёжаЕФЪ§ОнЙЙГЩЕФаТбљБОЕФЦНОљЪ§МЧЮЊ
ЃЈЕЅЮЛЃК аЁЪБЃЉЃЌетШ§ИіЪ§ОнгыБэИёжаЕФЪ§ОнЙЙГЩЕФаТбљБОЕФЦНОљЪ§МЧЮЊ![]() ЃЌБэИёжаЕФЪ§ОнЦНОљЪ§МЧЮЊ
ЃЌБэИёжаЕФЪ§ОнЦНОљЪ§МЧЮЊ![]() ЃЌЪдХаЖЯ
ЃЌЪдХаЖЯ![]() гы
гы![]() ЕФДѓаЁ. ЃЈНсТлВЛвЊЧѓжЄУїЃЉ
ЕФДѓаЁ. ЃЈНсТлВЛвЊЧѓжЄУїЃЉ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉжБНгИљОнЗжВуГщбљЗНЗЈЃЌПЩЕУИпШ§ФъМЖЕФНЬЪІЙВга![]() ЃЈШЫЃЉЃЛЃЈ2ЃЉИљОнЛЅГтЪТМўЁЂЖРСЂЪТМўЕФИХТЪЙЋЪНЧѓНтЃЛЃЈ3ЃЉЗжБ№ЧѓГіШ§зщзмЦНОљжЕ
ЃЈШЫЃЉЃЛЃЈ2ЃЉИљОнЛЅГтЪТМўЁЂЖРСЂЪТМўЕФИХТЪЙЋЪНЧѓНтЃЛЃЈ3ЃЉЗжБ№ЧѓГіШ§зщзмЦНОљжЕ![]() ЃЌвдМАаТМгШыЕФШ§ИіЪ§
ЃЌвдМАаТМгШыЕФШ§ИіЪ§![]() ЕФЦНОљЪ§ЮЊ9ЃЌБШНЯДѓаЁМДПЩ.
ЕФЦНОљЪ§ЮЊ9ЃЌБШНЯДѓаЁМДПЩ.
ЪдЬтНтЮіЃКЃЈ1ЃЉГщГіЕФ20ЮЛНЬЪІжаЃЌРДздИпШ§ФъМЖЕФга8УћЃЌ
ИљОнЗжВуГщбљЗНЗЈЃЌИпШ§ФъМЖЕФНЬЪІЙВга![]() ЃЈШЫЃЉ
ЃЈШЫЃЉ
ЃЈ2ЃЉЩшЪТМўЮЊ![]() ЁАМзЪЧЯжгабљБОжаИпвЛФъМЖжаЕФЕк
ЁАМзЪЧЯжгабљБОжаИпвЛФъМЖжаЕФЕк![]() ИіНЬЪІЁБЃЌ
ИіНЬЪІЁБЃЌ ![]() ЃЌ
ЃЌ
ЪТМў![]() ЁАввЪЧЯжгабљБОжаИпЖўФъМЖжаЕФЕк
ЁАввЪЧЯжгабљБОжаИпЖўФъМЖжаЕФЕк![]() ИіНЬЪІЁБЃЌ
ИіНЬЪІЁБЃЌ ![]() ЃЌ
ЃЌ
гЩЬтвтжЊЃК ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
![]()
ЩшЪТМў![]() ЮЊЁАИУжмМзЕФБИПЮЪБМфБШввЕФБИПЮЪБМфГЄЁБЃЌгЩЬтвтжЊЃЌ
ЮЊЁАИУжмМзЕФБИПЮЪБМфБШввЕФБИПЮЪБМфГЄЁБЃЌгЩЬтвтжЊЃЌ
![]()
Ыљвд![]()
![]()
ЙЪ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
![]()
Ш§зщзмЦНОљжЕ![]() ЃЌ
ЃЌ
аТМгШыЕФШ§ИіЪ§![]() ЕФЦНОљЪ§ЮЊ9ЃЌБШ
ЕФЦНОљЪ§ЮЊ9ЃЌБШ![]() аЁЃЌ
аЁЃЌ
ЙЪРЕЭСЫЦНОљжЕЃЌЁр![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЫФРтзЖSЉABCDЃЌЕзУцABCDЮЊСтаЮЃЌSAЁЭЦНУцABCDЃЌЁЯADC=60ЁуЃЌEЃЌFЗжБ№ЪЧSCЃЌBCЕФжаЕуЃЎ 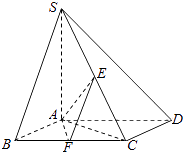
ЃЈ1ЃЉжЄУїЃКSDЁЭAFЃЛ
ЃЈ2ЃЉШєAB=2ЃЌSA=4ЃЌЧѓЖўУцНЧFЉAEЉCЕФгрЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈжЛЬюе§ШЗЫЕЗЈађКХЃЉ
ЂйШєМЏКЯA={y|y=xЉ1}ЃЌB={y|y=x2Љ1}ЃЌдђAЁЩB={ЃЈ0ЃЌЉ1ЃЉЃЌЃЈ1ЃЌ0ЃЉ}ЃЛ
Ђк ![]() ЪЧКЏЪ§НтЮіЪНЃЛ
ЪЧКЏЪ§НтЮіЪНЃЛ
Ђл ![]() ЪЧЗЧЦцЗЧХМКЏЪ§ЃЛ
ЪЧЗЧЦцЗЧХМКЏЪ§ЃЛ
ЂмЩшЖўДЮКЏЪ§fЃЈxЃЉ=ax2+bx+cЃЈaЁй0ЃЉЃЌШєfЃЈx1ЃЉ=fЃЈx2ЃЉЃЈx1Ёйx2ЃЉЃЌдђfЃЈx1+x2ЃЉ=cЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖЈвхдкRЩЯЕФКЏЪ§fЃЈxЃЉЪЧТњзуfЃЈxЃЉ+fЃЈЉxЃЉ=0ЃЌдкЃЈЉЁоЃЌ0ЃЉЩЯ ![]() ЃЌЧвfЃЈ5ЃЉ=0ЃЌдђЪЙfЃЈxЃЉЃМ0ЕФxШЁжЕЗЖЮЇЪЧ
ЃЌЧвfЃЈ5ЃЉ=0ЃЌдђЪЙfЃЈxЃЉЃМ0ЕФxШЁжЕЗЖЮЇЪЧ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЃК
ЃК ![]() ЃЈ
ЃЈ![]() ЃЉЕФзѓНЙЕу
ЃЉЕФзѓНЙЕу![]() гыХзЮяЯп
гыХзЮяЯп![]() ЕФНЙЕужиКЯЃЌжБЯп
ЕФНЙЕужиКЯЃЌжБЯп![]() гывддЕу
гывддЕу![]() ЮЊдВаФЃЌвдЭждВЕФРыаФТЪ
ЮЊдВаФЃЌвдЭждВЕФРыаФТЪ![]() ЮЊАыОЖЕФдВЯрЧаЃЎ
ЮЊАыОЖЕФдВЯрЧаЃЎ
ЃЈЂёЃЉЧѓИУЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈЂђЃЉЙ§Еу![]() ЕФжБЯпНЛЭждВгк
ЕФжБЯпНЛЭждВгк![]() ЃЌ
ЃЌ ![]() СНЕуЃЌЯпЖЮ
СНЕуЃЌЯпЖЮ![]() ЕФжаЕуЮЊ
ЕФжаЕуЮЊ![]() ЃЌ
ЃЌ ![]() ЕФДЙжБЦНЗжЯпгы
ЕФДЙжБЦНЗжЯпгы![]() жсКЭ
жсКЭ![]() жсЗжБ№НЛгк
жсЗжБ№НЛгк![]() ЃЌ
ЃЌ ![]() СНЕуЃЎМЧ
СНЕуЃЎМЧ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌ
ЃЌ ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЎЮЪЃКЪЧЗёДцдкжБЯп
ЃЎЮЪЃКЪЧЗёДцдкжБЯп![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌШєДцдкЃЌЧѓжБЯп
ЃЌШєДцдкЃЌЧѓжБЯп![]() ЕФЗНГЬЃЌШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЕФЗНГЬЃЌШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖЈвхгђЮЊRЕФКЏЪ§fЃЈxЃЉМШЪЧЦцКЏЪ§ЃЌгжЪЧжмЦкЮЊ3ЕФжмЦкКЏЪ§ЃЌЕБxЁЪЃЈ0ЃЌ ![]() ЃЉЪБЃЌfЃЈxЃЉ=sinІаxЃЌfЃЈ
ЃЉЪБЃЌfЃЈxЃЉ=sinІаxЃЌfЃЈ ![]() ЃЉ=0ЃЌдђКЏЪ§fЃЈxЃЉдкЧјМф[0ЃЌ6]ЩЯЕФСуЕуИіЪ§ЪЧЃЈ ЃЉ
ЃЉ=0ЃЌдђКЏЪ§fЃЈxЃЉдкЧјМф[0ЃЌ6]ЩЯЕФСуЕуИіЪ§ЪЧЃЈ ЃЉ
A.9
B.7
C.5
D.3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшУќЬтpЃКfЃЈxЃЉ= ![]() дкЧјМфЃЈ1ЃЌ+ЁоЃЉЩЯЪЧМѕКЏЪ§ЃЛУќЬтqЃЛx1x2ЪЧЗНГЬx2ЉaxЉ2=0ЕФСНИіЪЕИљЃЌВЛЕШЪНm2+5mЉ3Ён|x1Љx2|ЖдШЮвтЪЕЪ§ІСЁЪ[Љ1ЃЌ1]КуГЩСЂЃЛШєЉVpЁФqЮЊецЃЌЪдЧѓЪЕЪ§mЕФШЁжЕЗЖЮЇЃЎ
дкЧјМфЃЈ1ЃЌ+ЁоЃЉЩЯЪЧМѕКЏЪ§ЃЛУќЬтqЃЛx1x2ЪЧЗНГЬx2ЉaxЉ2=0ЕФСНИіЪЕИљЃЌВЛЕШЪНm2+5mЉ3Ён|x1Љx2|ЖдШЮвтЪЕЪ§ІСЁЪ[Љ1ЃЌ1]КуГЩСЂЃЛШєЉVpЁФqЮЊецЃЌЪдЧѓЪЕЪ§mЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§y=ax2+bxКЭЗДБШР§КЏЪ§ ![]() дкЭЌвЛзјБъЯЕжаЕФЭМЯѓДѓжТЪЧЃЈ ЃЉ
дкЭЌвЛзјБъЯЕжаЕФЭМЯѓДѓжТЪЧЃЈ ЃЉ
A.
B.
C.
D.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯжга![]() ЃЈnЁн2ЃЌnЁЪN*ЃЉИіИјЖЈЕФВЛЭЌЕФЪ§ЫцЛњХХГЩвЛИіЯТЭМЫљЪОЕФШ§НЧаЮЪ§еѓЃК
ЃЈnЁн2ЃЌnЁЪN*ЃЉИіИјЖЈЕФВЛЭЌЕФЪ§ЫцЛњХХГЩвЛИіЯТЭМЫљЪОЕФШ§НЧаЮЪ§еѓЃК

ЩшMkЪЧЕкkаажаЕФзюДѓЪ§ЃЌЦфжа1ЁмkЁмnЃЌkЁЪN*ЃЎМЧM1ЃМM2ЃМЁЃМMnЕФИХТЪЮЊpnЃЎ
ЃЈ1ЃЉЧѓp2ЕФжЕЃЛ
ЃЈ2ЃЉжЄУїЃКpnЃО![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com