
|


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
| x+1-a |
| a-x |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
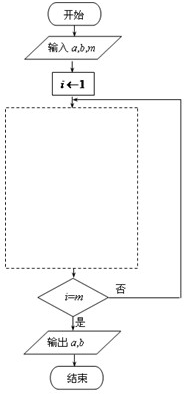 若数列{an},{bn}中,a1=a,b1=b,
若数列{an},{bn}中,a1=a,b1=b,
|
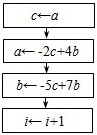 B、
B、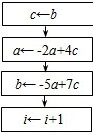
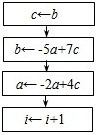 D、
D、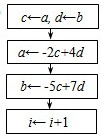
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| lim |
| n→∞ |
| lim |
| n→∞ |
查看答案和解析>>
科目:高中数学 来源:上海市虹口区2012届高三上学期期末教学质量监控测试数学试题 题型:044
已知Sn是数列{an}的前n项和,![]() (
(![]() ,
,![]() ),且
),且![]() .
.
(1)求a2的值,并写出an和an+1的关系式;
(2)求数列{an}的通项公式及Sn的表达式;
(3)我们可以证明:若数列{bn}有上界(即存在常数A,使得bn<A对一切n∈N*恒成立)且单调递增;或数列{bn}有下界(即存在常数B,使得bn>B对一切n∈N*恒成立)且单调递减,则![]() 存在.直接利用上述结论,证明:
存在.直接利用上述结论,证明:![]() 存在.
存在.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 (n≥2,n∈N*),且
(n≥2,n∈N*),且 .
.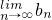 存在.直接利用上述结论,证明:
存在.直接利用上述结论,证明: 存在.
存在.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com