
分析 由平面向量基本定理判断①;举例说明②错误;由$\overrightarrow{MP}$=x$\overrightarrow{MA}$+y$\overrightarrow{MB}$,得$\overrightarrow{MP}$,$\overrightarrow{MA}$,$\overrightarrow{MB}$共面,即可得四点 P、M、A、B共面判断③.
解答 解:①若$\overrightarrow{p}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,则由平面向量基本定理得$\overrightarrow{p}$与$\overrightarrow{a}$、$\overrightarrow{b}$共面,故①正确;
②若$\overrightarrow{p}$与$\overrightarrow{a}$,$\overrightarrow{b}$共面,则$\overrightarrow{p}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$不一定成立,如$\overrightarrow{a}$,$\overrightarrow{b}$都是零向量,而$\overrightarrow{p}$为非零向量时,此等式不成立;
③若$\overrightarrow{MP}$=x$\overrightarrow{MA}$+y$\overrightarrow{MB}$,则$\overrightarrow{MP}$,$\overrightarrow{MA}$,$\overrightarrow{MB}$共面,∴四点 P、M、A、B共面,故③正确.
∴真命题的序号是①③.
故答案为:①③.
点评 本题考查命题的真假判断与应用,考查向量共线的基本概念,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{30}}{6}$ | B. | $\sqrt{7}$ | C. | $\frac{\sqrt{30}}{6}$或$\sqrt{7}$ | D. | $\frac{5}{6}$或7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
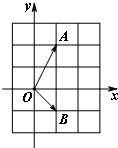
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com