
 为正三角形,
为正三角形, ,
, ,AC与BD交于O点.将
,AC与BD交于O点.将 沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为
沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为 ,且P点在平面ABCD内的射影落在
,且P点在平面ABCD内的射影落在 内.
内.
 平面PBD;
平面PBD; 时,求二面角
时,求二面角 的余弦值。
的余弦值。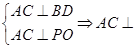 面PBD
面PBD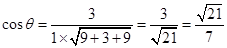
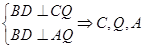 三点共线,即Q与O重合。
三点共线,即Q与O重合。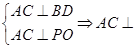 面PBD
面PBD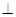 面PBD,而
面PBD,而 面ABCD,所以面ABCD
面ABCD,所以面ABCD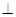 面PBD,则P点在面ABCD上的射影点在交线BD上(即在射线OD上),所以PO与平面ABCD所成的角
面PBD,则P点在面ABCD上的射影点在交线BD上(即在射线OD上),所以PO与平面ABCD所成的角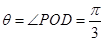 。以O为坐标原点,OA为
。以O为坐标原点,OA为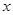 轴,OB为
轴,OB为 轴建空间直角坐标系。
轴建空间直角坐标系。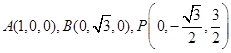 ,因为AC
,因为AC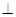 面PBD,所以面PBD的法向量
面PBD,所以面PBD的法向量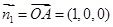 ,设面PAB的法向量
,设面PAB的法向量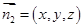 ,又
,又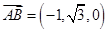 ,由
,由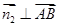 ,得
,得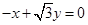 ①,又
①,又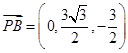 ,由
,由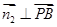 ,得
,得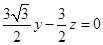 ②, 在①②中令
②, 在①②中令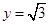 ,可得
,可得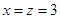 ,则
,则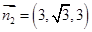
 的余弦值
的余弦值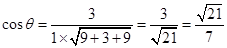


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源:不详 题型:解答题
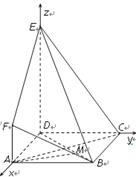
 是边长为
是边长为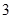 的正方形,
的正方形,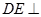 平面
平面 ,
, ,
,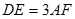 ,
,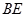 与平面
与平面 所成角为
所成角为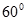 .
.
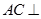 平面
平面 ;
;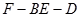 的余弦值;
的余弦值;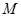 是线段
是线段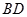 上一个动点,试确定点
上一个动点,试确定点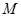 的位置,使得
的位置,使得 平面
平面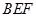 ,并证明你的结论.
,并证明你的结论.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
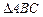 是边长为2的等边三角形,
是边长为2的等边三角形,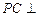 平面
平面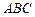 ,
,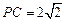 ,
,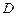 是
是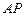 上一动点.
上一动点.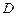 是
是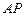 的中点,求直线
的中点,求直线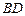 与平面
与平面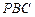 所成的角的正弦值;
所成的角的正弦值;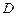 在运动过程中,是否有可能使
在运动过程中,是否有可能使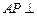 平面
平面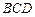 ?请说明理
?请说明理 由.
由.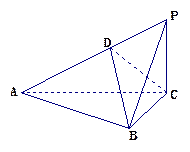
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com