
分析 (1)展开两数和的平方公式结合二倍角的正弦化简(sinx+cosx)2;利用二倍角正弦化简sinxcosxcos2x;展开平方差公式,结合平方关系及二倍角的余弦化简sin4x-cos4x;
(2)通分后利用倍角公式及两角差的正弦求解$\frac{1}{sin10°}$-$\frac{\sqrt{3}}{cos10°}$;化切为弦,再由两角差的正弦求解sin40°(tan10°-$\sqrt{3}$);利用两角和的正切化简$\frac{tan20°+tan40°+tan120°}{tan20°tan40°}$.
解答 解:(1)(sinx+cosx)2=sin2x+cos2x+2sinxcosx=1+sin2x;
sinxcosxcos2x=$\frac{1}{2}•2$sinxcosxcos2x=$\frac{1}{2}sin2xcos2x=\frac{1}{4}•2sin2xcos2x=\frac{1}{4}sin4x$;
sin4x-cos4x=(sin2x+cos2x)(sin2x-cos2x)=-cos2x.
故答案为:1+sin2x;$\frac{1}{4}sin4x$;-cos2x.
(2)$\frac{1}{sin10°}$-$\frac{\sqrt{3}}{cos10°}$=$\frac{cos10°-\sqrt{3}sin10°}{sin10°cos10°}$
=$\frac{-2(\frac{\sqrt{3}}{2}sin10°-\frac{1}{2}cos10°)}{sin10°cos10°}$=$\frac{-2sin(-20°)}{\frac{1}{2}sin20°}=4$;
sin40°(tan10°-$\sqrt{3}$)=$sin40°(\frac{sin10°}{cos10°}-\sqrt{3})$
=$sin40°•\frac{sin10°-\sqrt{3}cos10°}{cos10°}$=$sin40°•\frac{2sin(-50°)}{cos10°}$=$-\frac{sin80°}{cos10°}=-1$;
$\frac{tan20°+tan40°+tan120°}{tan20°tan40°}$=$\frac{tan20°+tan40°-tan60°}{tan20°tan40°}$
=$\frac{-tan60°tan40°tan20°}{tan20°tan40°}=-\sqrt{3}$.
点评 本题考查三角函数的化简求值,考查了三角函数中的恒等变换应用,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
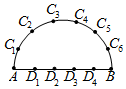 如图,在以AB为直径的半圆周上,有异于A、B的6个点C1、C2、C3、C4、C5、C6,线段AB上有异于A、B的四个点D1、D2、D3、D4.问:
如图,在以AB为直径的半圆周上,有异于A、B的6个点C1、C2、C3、C4、C5、C6,线段AB上有异于A、B的四个点D1、D2、D3、D4.问:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com