
设函数f(x)=Asin(ωx+ )(其中A>0,ω>0,-π<
)(其中A>0,ω>0,-π< ≤π)在x=
≤π)在x=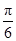 处取得最大值2,其图象与x轴的相邻两个交点的距离为
处取得最大值2,其图象与x轴的相邻两个交点的距离为 .
.
(1)求f(x)的解析式;
(2)求函数g(x)=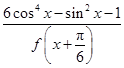 的值域.
的值域.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
已知向量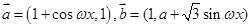 (
(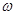 为常数且
为常数且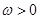 ),函数
),函数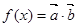 在
在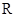 上的最大值为
上的最大值为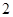 .
.
(1)求实数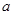 的值;
的值;
(2)把函数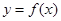 的图象向右平移
的图象向右平移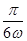 个单位,可得函数
个单位,可得函数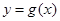 的图象,若
的图象,若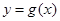 在
在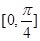 上为增函数,求
上为增函数,求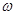 取最大值时的单调增区间.
取最大值时的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设平面向量a=(cosx,sinx),b=(cosx+2 ,sinx),x∈R.
,sinx),x∈R.
(1)若x∈(0, ),证明:a和b不平行;
),证明:a和b不平行;
(2)若c=(0,1),求函数f(x)=a·(b-2c)的最大值,并求出相应的x值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某兴趣小组要测量电视塔AE的高度H(单位:m)如图所示,垂直放置的标杆BC的高度h=4m,仰角∠ABE=α,∠ADE=β.
(1)该小组已测得一组α、β的值,算出了tanα=1.24,tanβ=1.20,请据此算出H的值;
(2)该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使α与β之差较大,可以提高测量精度.若电视塔的实际高度为125m,试问d为多少时,α-β最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知关于x的方程2x2-( +1)x+m=0的两根为sinθ和cosθ,且θ∈(0,2π).
+1)x+m=0的两根为sinθ和cosθ,且θ∈(0,2π).
(1)求 的值;
的值;
(2)求m的值;
(3)求方程的两根及此时θ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=sin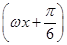 +
+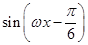 -2cos2
-2cos2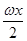 ,x∈R(其中ω>0).
,x∈R(其中ω>0).
(1)求函数f(x)的值域;
(2)若函数y=f(x)的图象与直线y=-1的两个相邻交点间的距离为 ,求函数y=f(x)的单调增区间.
,求函数y=f(x)的单调增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com