
 在如图所示的多面体ABCDEF中,ABCD为直角梯形,AB∥CD,∠DAB=90°,四边形ADEF为等腰梯形,EF∥AD,已知AE⊥EC,AB=AF=EF=2,AD=CD=4.
在如图所示的多面体ABCDEF中,ABCD为直角梯形,AB∥CD,∠DAB=90°,四边形ADEF为等腰梯形,EF∥AD,已知AE⊥EC,AB=AF=EF=2,AD=CD=4.分析 (Ⅰ)取AD中点M,连接EM,只需证明AE⊥CD,CD⊥AD,即可得CD⊥平面ADEF.
(Ⅱ)作EO⊥AD,可得EO=$\sqrt{3}$,连接AC,则VABCDEF=VC-ADEF+VF-ABC,
解答 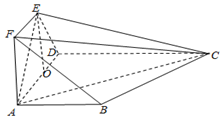 解:(Ⅰ)证明:取AD中点M,连接EM,
解:(Ⅰ)证明:取AD中点M,连接EM,
∵AF=EF=DE=2,AD=4,可知EM=$\frac{1}{2}$AD,∴AE⊥DE,
又AE⊥EC,DE∩EC=E∴AE⊥平面CDE,
∵CD?平面CDE,∴AE⊥CD,
又CD⊥AD,AD∩AE=A,∴CD⊥平面ADEF.
(Ⅱ)由(1)知 CD⊥平面ADEF,CD?平面ABCD,
∴平面ABCD⊥平面ADEF;
作EO⊥AD,∴EO⊥平面ABCD,EO=$\sqrt{3}$,连接AC,则VABCDEF=VC-ADEF+VF-ABC,
${V_{C-ADEF}}=\frac{1}{3}•{S_{ADEF}}•CD=\frac{1}{3}×\frac{1}{2}×(2+4)×\sqrt{3}×4=4\sqrt{3}$,${V_{F-ABC}}=\frac{1}{3}•{S_{△ABC}}•OE=\frac{1}{3}×\frac{1}{2}×2×4×\sqrt{3}=\frac{{4\sqrt{3}}}{3}$,
∴${V_{ABCDEF}}=4\sqrt{3}+\frac{{4\sqrt{3}}}{3}=\frac{{16\sqrt{3}}}{3}$.
点评 本题考查了空间线线、线面、面面位置关系,几何体体积计算,属于中档题,


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{8}{45}$ | C. | $\frac{4}{5}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | a<b<c | C. | c<a<b | D. | a<c<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{π}{12},0}]$ | B. | $({-\frac{π}{8},-\frac{π}{24}}]$ | C. | $[-\frac{π}{12},\frac{π}{8})$ | D. | $[{0,\frac{π}{12}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -454 | B. | -450 | C. | -446 | D. | -442 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y平均增加1.5个单位 | B. | y平均增加0.5个单位 | ||
| C. | y平均减少1.5个单位 | D. | y平均减少0.5个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com