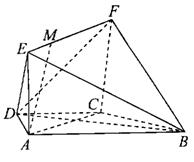
如图，在梯形ABCD中，AB//CD，AD=DC=CB=a，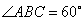
，四边形ACFE是矩形，且平面
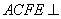平面ABCD，点M在线段EF上．
（I）求证：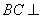
平面ACFE；
（II）当EM为何值时，AM//平面BDF？证明你的结论．
名校课堂系列答案科目：高中数学 来源： 题型：
在平面几何中有如下结论：若正三角形ABC的内切圆面积为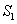
，外接圆面积为
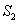，则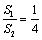
．推广到空间几何体中可以得到类似结论：若正四面体ABCD的内切球体积为
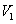，外接球体积为
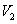，则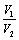
=___________．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知方程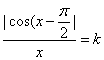
在（0，+∞）上有两个不同的解a，b（a＜b），则下面结论正确的是 （ ）
A．sina=acosb B．sina=-acosb C．cosa=bsinb D．sinb=-bsina
查看答案和解析>>
科目：高中数学 来源： 题型：
校运动会招聘志愿者，甲、乙、丙三名大学生跃跃欲试，已知甲能被录用的概率是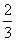
，甲、乙两人都不能被录用的概率为
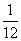，丙、乙两人都能被录用的概率为
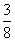，且三人是否录用相互独立。
⑴求乙、丙两人各自能被录用的概率；
⑵求甲、乙、丙三人至少有两人能被录用的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
中，
， 
，
四边形
且
，
，
． …………3分
平面
平面
，
平面
． …………6分
时，
平面
， ……7分
，连接
，则
， 
，而
， 
， …………9分
， 
是平行四边形，
， 
平面
，
平面
平面
.
处的切线为
，
的值；
的单调区间；
，求证：在
时，
=2lnx+
在x=1处的切线方程是 .
顶点在坐标原点O，始边
轴的非负半轴重合，点P在
，且
夹角的余弦值为 （ ）
B．
C．
D．
，
，则
与
夹角的余弦值为 （ ）
B．
C．
D．