
分析 (1)求导数,利用导数的正负,即可证明结论;
(2)利用复合函数的单调性求解,先将函数转化为两个基本函数,由同增异减的结论求解.
解答 证明:(1)f′(x)=1-$\frac{a}{{x}^{2}}$,令f′(x)>0,则1-$\frac{a}{{x}^{2}}$>0,
解得x>$\sqrt{a}$或x<-$\sqrt{a}$(舍).
令f′(x)<0,则1-$\frac{a}{{x}^{2}}$<0,
解得-$\sqrt{a}$<x<$\sqrt{a}$.
∵x>0,∴0<x<$\sqrt{a}$.
∴f(x)在(0,$\sqrt{a}$)上为减函数;在($\sqrt{a}$,+∞)上为增函数,
也称为f(x)在(0,$\sqrt{a}$]上为减函数;在[$\sqrt{a}$,+∞)上为增函数.
解:(2)令u=x2-4x+3,原函数可以看作y=log${\;}_{\frac{1}{3}}$u与u=x2-4x+3的复合函数.
令u=x2-4x+3>0.
则x<1或x>3.
∴函数y=log${\;}_{\frac{1}{3}}$(x2-4x+3)的定义域为(-∞,1)∪(3,+∞).
又u=x2-4x+3的图象的对称轴为x=2,且开口向上,
∴u=x2-4x+3在(-∞,1)上是减函数,在(3,+∞)上是增函数.
而函数y=log${\;}_{\frac{1}{3}}$u在(0,+∞)上是减函数,
∴y=log${\;}_{\frac{1}{3}}$(x2-4x+3)的单调递减区间为(3,+∞),单调递增区间为(-∞,1).
点评 本题主要利用导数证明函数的单调性,考查复合函数的单调性,结论是同增异减,一定要注意定义域.


科目:高中数学 来源: 题型:选择题
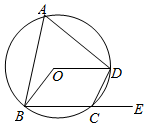
| A. | 120° | B. | 136° | C. | 144° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
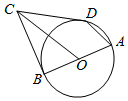 如图所示,AB是圆O的直径,BC与圆O相切于B,∠ADC+∠DCO=180°
如图所示,AB是圆O的直径,BC与圆O相切于B,∠ADC+∠DCO=180°查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 圆与直线相切 | B. | 圆与直线相交 | ||
| C. | 圆与直线相离 | D. | 以上三种均有可能 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com