
分析 (Ⅰ)求出f(x)的导数,计算f′(1),求出切线方程即可;
(Ⅱ)求出F(x)的导函数,把原函数有两个极值点转化为h(x)=x2-2ax+1在(0,+∞)上有两个相异零点x1,x2.由此结合二次函数根的分布求得a的范围.进一步得到m=$\frac{{x}^{2}+1}{2x}$,代入f(x),利用导数求得f(x2)<-1<f(x1).
解答 (Ⅰ)解:m=1时,f(x)=x(lnx-x),f′(x)=lnx-2x+1,
故f′(1)=-1,
故切线方程是:y+1=-(x-1),
即x+y=0;
(Ⅱ)证明:∵F(x)=lnx-2mx+1+$\frac{1}{2}$x2,
∴F′(x)=$\frac{1}{x}$-2mx+x=$\frac{{x}^{2}-2mx+1}{x}$,
函数F(x)有两个极值点x1,x2,
即h(x)=x2-2mx+1在(0,+∞)上有两个相异零点x1,x2.
∵x1x2=1>0,∴$\left\{\begin{array}{l}{△={4a}^{2}-4>0}\\{{x}_{1}{+x}_{2}=2m>0}\end{array}\right.$,则m>1.
当0<x<x1 或x>x2时,F′(x)>0,当x1<x<x2时,F′(x)<0,
∴F(x)在(0,x1),(x2,+∞)上单调递增,在(x1,x2)上单调递减;
∵h(1)=2-2m<0,∴0<x1<1<m<x2,
令x2-2mx+1=0,得m=$\frac{{x}^{2}+1}{2x}$,
∴f(x)=x(lnx-mx)=xlnx-$\frac{1}{2}$x3-$\frac{1}{2}$x,则f′(x)=lnx-$\frac{3}{2}$x2+$\frac{1}{2}$,
设s(x)=lnx-$\frac{3}{2}$x2+$\frac{1}{2}$,s′(x)=$\frac{1}{x}$-3x=$\frac{1-{3x}^{2}}{x}$,
①当x>1时,s′(x)<0,s(x)在(1,+∞)上单调递减,
从而s(x)在(m,+∞)上单调递减,
∴s(x)<s(m)<s(1)=-1<0,
∴f(x)在(1,+∞)上单调递减,
∴f(x)<f(1)=-1<0,
∵1<m<x2,∴f(x2)<-1;
②当0<x<1时,由s′(x)>0,得0<x<$\frac{\sqrt{3}}{3}$,
由s′(x)<0,得$\frac{\sqrt{3}}{3}$<x<1,∴s(x)在(0,$\frac{\sqrt{3}}{3}$)上单调递增,在($\frac{\sqrt{3}}{3}$,1)上单调递减,
∴s(x)≤s($\frac{\sqrt{3}}{3}$)=ln$\frac{\sqrt{3}}{3}$<0,∴f(x)在(0,1)上单调递减,则f(x)>f(1)=-1,
∵x1∈(0,1),∴f(x1)>-1.
综上可知:f(x2)<-1<f(x1).
点评 本题考查利用导数研究过曲线上某点处的切线方程,考查利用导数求函数的最值,训练了利用导数证明函数不等式问题,对于(Ⅱ)的证明,着重考查了分类讨论的数学思想方法,运用了二次函数零点所在区间的判断,题目设置难度大,综合型强,是压轴题.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)是奇函数,函数g(x)是偶函数 | |
| B. | 函数f(x)不是奇函数,函数g(x)是偶函数 | |
| C. | 函数f(x)是奇函数,函数g(x)不是偶函数 | |
| D. | 函数f(x)不是奇函数,函数g(x)不是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,+∞) | B. | (-3,+∞) | C. | (-∞,3) | D. | (-∞,-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
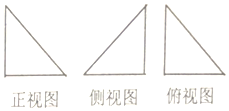 一几何体的三视图如图所示,三个三角形都是直角边为2的等腰直角三角形,该几何体的顶点都在球O上,球O的表面积为( )
一几何体的三视图如图所示,三个三角形都是直角边为2的等腰直角三角形,该几何体的顶点都在球O上,球O的表面积为( )| A. | 16π | B. | 3π | C. | $4\sqrt{3}π$ | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com