
���� ��1������C�ļ����귽��Ϊ2��2cos2��-3��2sin2��=30����y=��sin�ȣ�x=��cos�ȴ��뼴�ɻ�Ϊ�����̣��ɵ�c=5���õ�ԲO�İ뾶Ϊ5�����ɵó������̣�
��2����ֱ��l�IJ�������$\left\{\begin{array}{l}x=4+tcos��\\ y=-3+tsin��\end{array}$��tΪ����������֪��ֱ��l������B��4��-3������B��ԲO�ϣ���|BC|=5���ɵá�OBC�ǵȱ������Σ��ó�sin��xOB���ɵó�sin��$\frac{��}{3}$-������
���  �⣺��1������C�ļ����귽��Ϊ2��2cos2��-3��2sin2��=30��
�⣺��1������C�ļ����귽��Ϊ2��2cos2��-3��2sin2��=30��
��y=��sin�ȣ�x=��cos�ȴ��뼴�ɻ�Ϊ2x2-3y2=30���������Ϊ��$\frac{{x}^{2}}{15}-\frac{{y}^{2}}{10}=1$��
��c=$\sqrt{15+10}$=5��
�ɵ�����C���ҽ���F��5��0����
��ԲO�ı�����Ϊ��x2+y2=25��
��2����ֱ��l�IJ�������$\left\{\begin{array}{l}x=4+tcos��\\ y=-3+tsin��\end{array}$��tΪ��������
��֪��ֱ��l������B��4��-3����
��B��ԲO�ϣ���|BC|=5�����OBC�ǵȱ������Σ�
��sin��xOB=$\frac{3}{5}$
��sin��$\frac{��}{3}$-����=$\frac{3}{5}$��
���� ���⿼���˼�������ֱ�����귽�̵Ļ������������̻�Ϊ��ͨ���̡�ֱ����Բ�ཻ�ҳ����ȱ������ε����ʣ�������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|x��7��x��-3} | B�� | {x|-3��x��7} | C�� | {x|-7��x��3} | D�� | {x|x��-3} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ȷ����ϵ | B�� | F+E-V=2 | C�� | E+V-F=2 | D�� | F+V-E=2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
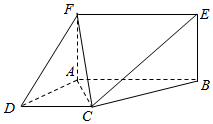 ��ͼ����֪�ı���ABEFΪ���Σ��ı���ABCDΪֱ�����Σ�ƽ��ABEF��ƽ��ABCD����BAD=90�㣬AB��CD��AF=BC=2��CD=3��AB=4��
��ͼ����֪�ı���ABEFΪ���Σ��ı���ABCDΪֱ�����Σ�ƽ��ABEF��ƽ��ABCD����BAD=90�㣬AB��CD��AF=BC=2��CD=3��AB=4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | K2��ֵ����Ϊ��ֵ | |
| B�� | K2�����Լ����ͳ�Ƽ����Ǹ��¼�֮������� | |
| C�� | K2�����Լ�����ʾ������������������ϰ���йء���ָ��������ϰ�ߵ��˱ػỼ���������ס� | |
| D�� | 2��2�������е�4�����ݿ�Ϊ�κ�ʵ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
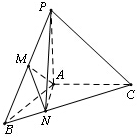 ��ͼ��������P-ABC�У�PA����ABC����BAC=120�㣬��AB=AC=AP=1��MΪPB���е㣬N��BC�ϣ���BN=$\frac{1}{3}$BC��
��ͼ��������P-ABC�У�PA����ABC����BAC=120�㣬��AB=AC=AP=1��MΪPB���е㣬N��BC�ϣ���BN=$\frac{1}{3}$BC���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com