练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知数列{an}中，a1=1,an+1=(an+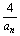)(n∈N*),且{an}存在极限。

    （1）证明：{an}时先增后减数列，并求an的最大值；

    （2）已知圆锥曲线Cn的方程为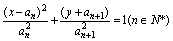：设Cn=C,求曲线C的方程并求曲线C的面积。


     得an=an-1=…=an=a1=2，这与条件矛盾，因此，an≠2对n∈N*恒成立. ∴当n≥2时，an>2.

    又n≥2时，

    an-an+1=an-

    ∴a1,<a2,a2<a3>…an>an+1>…>2,即{an}是行列增后减数列，（an）max=a2=


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知函数f(x)=ax3+bx2-3x在x=±1处有极值。

    （1）讨论f(1)和f(-1)是函数的极大值还是极小值。

    （2）过点A（0，16）作曲线y=f(x)的切线，求此切线方程。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     已知函数y=Asin(w+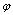)(x∈R)(其中A>O,w>0)的图像在y轴右侧的第一个最高点为M(2，2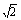)，与x轴在原点右侧的第一个交点为N(0,0)

    (1)求这个函数的解析式；

     (2)此函数可以由y=sinx经过怎样的变换得到?(写出每一个具体变换)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若（）=1，则常数a,b的值为   （ ）

    A．a=-2,b=4           B．a=2,b=-4

    C．a=-1,b=-4          D．a=2,b=4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)=logax(a>0且a≠1),若数列：2，f(a1),f(2),…,f(an),2n+4(n∈N*)成等差数列。

    （1）求数列{an}的通项an;

     (2)若0<a<1,数列{an}的前n项和为Sn,求Sn;

     (3)若a=2,令bn=an·f(an),对任意n∈N*，都有bn>f-1(t),求实数t的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知点A

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知点P(x,y)在不等式组  

    A．[-2，-1]          B.[-2,1]

    C.[-1,2]             D.[1,2]

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    直线与直线，直线分别交于两点，中点为，则直线的斜率是（    ）

    A、          B、             C、          D、

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图11-1，四棱锥P—ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=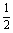AB=1，M是PB的中点。

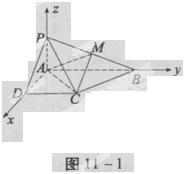
    （1）证明：面PAD⊥面PCD；

    （2）求AC与PB所成的角；

    （3）求面AMC与面BMC所成二面角A-CM-B的大小。

    查看答案和解析>>

    同步练习册答案