
【题目】已知![]() .
.
(1)若![]() 有两个零点,求
有两个零点,求![]() 的范围;
的范围;
(2)若![]() 有两个极值点,求
有两个极值点,求![]() 的范围;
的范围;
(3)在(2)的条件下,若![]() 的两个极值点为
的两个极值点为![]()
![]() ,求证:
,求证: ![]() .
.
【答案】(1) ![]() (2)
(2) ![]() (3) 见解析
(3) 见解析
【解析】试题分析:(1)由题意函数![]() 必有极值点,且极大值大于零,列对应不等式,解得
必有极值点,且极大值大于零,列对应不等式,解得![]() 的范围;(2)先求导数,得
的范围;(2)先求导数,得![]() 有两个改变
有两个改变![]() 符号的零点,即导函数
符号的零点,即导函数![]() 必有极值点,且极大值大于零,列对应不等式,解得
必有极值点,且极大值大于零,列对应不等式,解得![]() 的范围;(3)由(2)
的范围;(3)由(2)![]() 再利用极值点条件构造函数
再利用极值点条件构造函数![]() ,最后利用导数研究函数单调性,根据最值证不等式
,最后利用导数研究函数单调性,根据最值证不等式
试题解析:方法一:
(1)![]()
![]() 有两个零点,
有两个零点, ![]() 有两个零点
有两个零点
![]()
![]() 时
时![]() 在
在![]() 上单调,最多有一个零点,不合题意
上单调,最多有一个零点,不合题意
![]() 在
在![]() 上↑,在
上↑,在![]() 上↓
上↓
![]()
又![]() 时,
时, ![]()
![]() 必有两个零点
必有两个零点
![]()
(2)![]()
![]() 符号的零点
符号的零点
设![]() 则
则![]()
![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 在
在![]() 上单调,最多有一个零点,不合题意
上单调,最多有一个零点,不合题意
![]() 由
由![]() 得:
得: ![]() ,
,
![]() 在
在![]() 上↑,在
上↑,在![]() 上↓
上↓
![]() ,即
,即![]()
又![]()
![]() 在
在![]() 各有一个零点
各有一个零点
![]()
(3)由(2),结合h(1)=1-2a>0,知![]()
![]()
设![]()
![]() 在
在![]() 上↓,
上↓,![]()
![]()
方法二:分离参数法
(1)![]() ,两图象有两交点
,两图象有两交点
令![]()
当![]()
当![]() ,
, ![]()
结合图像, ![]() 。
。
(2)![]() 有两个改变
有两个改变![]() 符号的零点
符号的零点
等价于![]() 对应的两函数的图像有两交点
对应的两函数的图像有两交点
令![]()
当![]()
当![]()
结合图象, ![]()
(3)由(2)![]()
![]()


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
【题目】某段地铁线路上有A,B,C三站,![]() (千米),
(千米),![]() (千米),在列车运行时刻表上,规定列车8:00从A站出发,8:07到达B站,并停留1分钟,8:12到达C站,并在行驶时以同一速度
(千米),在列车运行时刻表上,规定列车8:00从A站出发,8:07到达B站,并停留1分钟,8:12到达C站,并在行驶时以同一速度![]() (千米/分)匀速行驶;列车从A站出发到达某站的时间与时刻表上相应时间差的绝对值,称为列车在该站的运行误差;
(千米/分)匀速行驶;列车从A站出发到达某站的时间与时刻表上相应时间差的绝对值,称为列车在该站的运行误差;
(1)分别用速度![]() 表示列车在B,C两站的运行误差;
表示列车在B,C两站的运行误差;
(2)若要求列车在B,C两站的运行误差之和不超过2分钟,求列车速度![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色.如图,某摩天轮最高点距离地面高度为120m,转盘直径为110m,设置有48个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周大约需要30min.

(1)游客甲坐上摩天轮的座舱,开始转动tmin后距离地面的高度为Hm,求在转动一周的过程中,H关于t的函数解析式;
(2)求游客甲在开始转动5min后距离地面的高度;
(3)若甲、乙两人分别坐在两个相邻的座舱里,在运行一周的过程中,求两人距离地面的高度差h(单位:m)关于t的函数解析式,并求高度差的最大值(精确到0.1).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小区抽取50户居民进行月用电量调查,发现其用电量都在50到350度之间,将用电量的数据绘制成频率分布直方图如下.
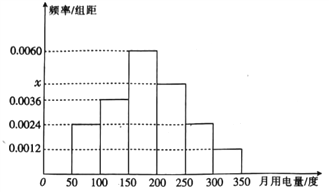
(1)求频率分布直方图中![]() 的值并估计这50户用户的平均用电量;
的值并估计这50户用户的平均用电量;
(2)若将用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为低用电家庭,用电量在区间
类用户,标记为低用电家庭,用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图:
类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图:
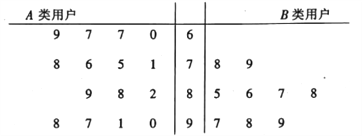
①从![]() 类用户中任意抽取3户,求恰好有2户打分超过85分的概率;
类用户中任意抽取3户,求恰好有2户打分超过85分的概率;
②若打分超过85分视为满意,没超过85分视为不满意,请填写下面列联表,并根据列联表判断是否有![]() 的把握认为“满意度与用电量高低有关”?
的把握认为“满意度与用电量高低有关”?
满意 | 不满意 | 合计 | |
| |||
| |||
合计 |
附表及公式:
| <>0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
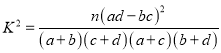 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)在已分组的若干数据中,每组的频数是指___________,每组的频率是指____________.
(2)一个公司共有N名员工,下设一些部门,要采用等比例外层随机抽样的方法从全体员工中抽取样本量为n的样本,如果某部门有m名员工,那么从该部门抽取的员工人数是____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点与直角坐标系的原点重合,极轴与![]() 轴的非负半轴重合.若曲线
轴的非负半轴重合.若曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为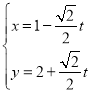 (
(![]() 为参数).
为参数).
(Ⅰ)求曲线![]() 的直角坐标方程与直线
的直角坐标方程与直线![]() 的普通方程;
的普通方程;
(Ⅱ)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com