考点:利用导数求闭区间上函数的最值,函数解析式的求解及常用方法
专题:数形结合法,导数的综合应用
分析:(1)求抽象函数g(x)的解析式,运用了方程的思想;而h(x)是具体函数,可以直接设出来,用待定系数法求之.
(2)ϕ(x)≥F(x)恒成立,即:ϕ(x)min≥F(x)max,利用导数分别求出ϕ(x)和F(x)的最小值和最大值.
(3)利用数形结合,对参数进行讨论求出方程的根的个数.
解答:
解:(Ⅰ)∵
g(x)+2g(-x)=ex+-9,①,在①中以-x代替x得:
g(-x)+2g(x)=e-x+-9,即
g(-x)+2g(x)=2ex+-9,②
由①②联立解得:g(x)=e
x-3.
∵h(x)是二次函数,且h(-2)=h(0)=1,可设h(x)=ax(x+2)+1,
由h(-3)=-2,解得a=-1.
∴h(x)=-x(x+2)+1=-x
2-2x+1,
∴g(x)=e
x-3,h(x)=-x
2-2x+1.
(Ⅱ)设ϕ(x)=h(x)+ax+5=-x
2+(a-2)x+6,F(x)=e
x-3-x(e
x-3)=(1-x)e
x+3x-3,
依题意知:当-1≤x≤1时,ϕ(x)
min≥F(x)
max,
∵F′(x)=-e
x+(1-x)(e
x-3)+3=-xe
x+3,在[-1,1]上单调递减,∴F′(x)
min=F′(1)=3-e>0,
∴F(x)在[-1,1]上单调递增,
∴F(x)
max=F(1)=0,
∴
,解得:-3≤a≤7,
∴实数a的取值范围为[-3,7].
(Ⅲ)当f(x)>0时,有e
f(x)-3=2,则f(x)=ln5,
当f(x)≤0时,有=-f(x)
2-2f(x)+1=2,则f(x)=-1,
即若f[f(x)]=2,则有f(x)=-1或f(x)=ln5,
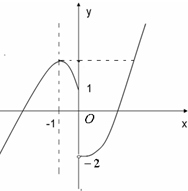
而f(x)的图象如图所示:
y=f(x)与y=-1有2个交点,与y=ln5有1个交点,
则f[f(x)]=2共有3个解.
点评:本题考查了:求函数解析式的方法,运用方程思想求抽象函数解析式,用待定系数法求具体函数解析式;利用最值解决恒成立问题;利用数结合法解决方程根的个数问题.这些问题都是我们经常遇到的,所以在平时应多多注意.这是一道综合性很强的导数试题.难度较大.




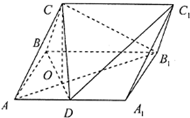 在三棱柱ABC-A1B1C1中,侧面ABBA1为矩形,AB=1,AA1=
在三棱柱ABC-A1B1C1中,侧面ABBA1为矩形,AB=1,AA1=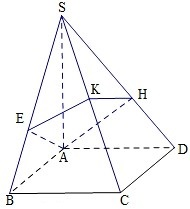 如图,四棱锥S-ABCD的底面是正方形,侧棱SA⊥底面ABCD,过A作AE垂直SB交SB于E点,作AH垂直SD交SD于H点,平面AEH交SC于K点,且AB=1,SA=2.
如图,四棱锥S-ABCD的底面是正方形,侧棱SA⊥底面ABCD,过A作AE垂直SB交SB于E点,作AH垂直SD交SD于H点,平面AEH交SC于K点,且AB=1,SA=2.