
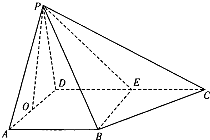
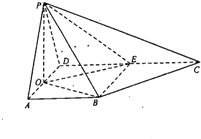
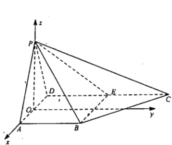
 如图,在四棱锥P-ABCD中,已知AB⊥AD,PA=PD,D为AD的中点,AB⊥PO,E为线段DC上一点,向量
如图,在四棱锥P-ABCD中,已知AB⊥AD,PA=PD,D为AD的中点,AB⊥PO,E为线段DC上一点,向量| DE |
| AB |
| 3 |
| 2 |
| 7 |
| 21 |
| DE |
| AB |
| 3 |
| DE |
| AB |
| PA |
| 3 |
| PD |
| 3 |
| PB |
| 3 |
| BE |
| PC |
| 3 |
| n |
| n |
| PB |
| n |
| BE |
| n |
| 3 |
|
| ||||
|
|
|
| ||||
|
| 2 |
| 7 |
| 21 |
| PC |
| 3 |
| m |
| m |
| PB |
| m |
| PC |
| m |
| ||
| 3 |
| ||
| 3 |
| 3 |
| m |
| 3 |
| AB |
| AB |
| m |
| ||||
|
|
| 2 | ||
|
| ||
| 5 |
| ||
| 5 |


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
 如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,且AE=EF=FB=5,DE=12,动点P从点A出发,沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止,设运动时间为t秒,y=S△EPF,则y与t的函数图象大致是( )
如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,且AE=EF=FB=5,DE=12,动点P从点A出发,沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止,设运动时间为t秒,y=S△EPF,则y与t的函数图象大致是( )A、 |
B、 |
C、 |
D、 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| n |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 2013年12月26日上午,日本首相安倍晋三参拜了靖国神社.这是安倍两次出任首相以来首次参拜,引起周边国家的强烈谴责,我军为了加强防范外敌入侵加强军事演习.在某次军事演习中红方为了准确分析战场形势,在两个相距为
2013年12月26日上午,日本首相安倍晋三参拜了靖国神社.这是安倍两次出任首相以来首次参拜,引起周边国家的强烈谴责,我军为了加强防范外敌入侵加强军事演习.在某次军事演习中红方为了准确分析战场形势,在两个相距为
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,斜三棱柱ABC-A1B1C1的所有棱长都为2,侧面AA1BB1⊥底面ABC,D为CC1中点,E为A1B1的中点,∠ABB1=60°.
如图,斜三棱柱ABC-A1B1C1的所有棱长都为2,侧面AA1BB1⊥底面ABC,D为CC1中点,E为A1B1的中点,∠ABB1=60°.查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 5 |
| 2 |
| a-1 |
| x |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 6 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱,污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米.已知流出的水中该杂质的质量分数与a,b的乘积ab成反比,现有制箱材料60平方米.(注:制箱材料必须用完)
如图所示,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱,污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米.已知流出的水中该杂质的质量分数与a,b的乘积ab成反比,现有制箱材料60平方米.(注:制箱材料必须用完)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com