
 如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,且AE=EF=FB=5,DE=12,动点P从点A出发,沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止,设运动时间为t秒,y=S△EPF,则y与t的函数图象大致是( )
如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,且AE=EF=FB=5,DE=12,动点P从点A出发,沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止,设运动时间为t秒,y=S△EPF,则y与t的函数图象大致是( )A、 |
B、 |
C、 |
D、 |
| AE2+DE2 |
| BF2+CF2 |

| 12 |
| 13 |
| 1 |
| 2 |
| 30 |
| 13 |
| 1 |
| 2 |
| 12 |
| 13 |
| 12(31-t) |
| 13 |
| 12(31-t) |
| 13 |


科目:高中数学 来源: 题型:
|
| A、x-y-3=0 |
| B、x+2y=5 |
| C、x+y-1=0 |
| D、2x-y-5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、命题“若am2<bm2,则a<b”的逆命题是真命题 | ||||
| B、在△ABC中,若acosA=bcosB,则△ABC为等腰直角三角形 | ||||
| C、命题“?x∈R,x2-x>0”的否定是:“?x∈R,x2-x≤0” | ||||
D、为得到函数y=sin(2x-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
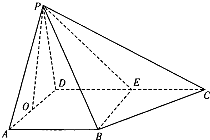 如图,在四棱锥P-ABCD中,已知AB⊥AD,PA=PD,D为AD的中点,AB⊥PO,E为线段DC上一点,向量
如图,在四棱锥P-ABCD中,已知AB⊥AD,PA=PD,D为AD的中点,AB⊥PO,E为线段DC上一点,向量| DE |
| AB |
| 3 |
| 2 |
| 7 |
| 21 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com