
 如图所示,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱,污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米.已知流出的水中该杂质的质量分数与a,b的乘积ab成反比,现有制箱材料60平方米.(注:制箱材料必须用完)
如图所示,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱,污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米.已知流出的水中该杂质的质量分数与a,b的乘积ab成反比,现有制箱材料60平方米.(注:制箱材料必须用完)
|
|
| a•2b |
| 2ab |
| 2ab |
| ab |
| 2 |
| ab |
| 2 |
| ab |
| ab |
| 2 |
|
|


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
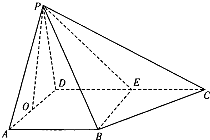 如图,在四棱锥P-ABCD中,已知AB⊥AD,PA=PD,D为AD的中点,AB⊥PO,E为线段DC上一点,向量
如图,在四棱锥P-ABCD中,已知AB⊥AD,PA=PD,D为AD的中点,AB⊥PO,E为线段DC上一点,向量| DE |
| AB |
| 3 |
| 2 |
| 7 |
| 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com