
 2013年12月26日上午,日本首相安倍晋三参拜了靖国神社.这是安倍两次出任首相以来首次参拜,引起周边国家的强烈谴责,我军为了加强防范外敌入侵加强军事演习.在某次军事演习中红方为了准确分析战场形势,在两个相距为
2013年12月26日上午,日本首相安倍晋三参拜了靖国神社.这是安倍两次出任首相以来首次参拜,引起周边国家的强烈谴责,我军为了加强防范外敌入侵加强军事演习.在某次军事演习中红方为了准确分析战场形势,在两个相距为
| ||
| 2 |
| DCsin30° |
| sin45° |
| ||
| 4 |
| ||
| 2 |
| AC2+BC2-2AC•BCcos45° |
|


科目:高中数学 来源: 题型:
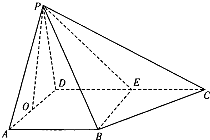 如图,在四棱锥P-ABCD中,已知AB⊥AD,PA=PD,D为AD的中点,AB⊥PO,E为线段DC上一点,向量
如图,在四棱锥P-ABCD中,已知AB⊥AD,PA=PD,D为AD的中点,AB⊥PO,E为线段DC上一点,向量| DE |
| AB |
| 3 |
| 2 |
| 7 |
| 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com