
【题目】已知向量 ![]() =(sinx,cosx),
=(sinx,cosx), ![]() =(sin(x﹣
=(sin(x﹣ ![]() ),sinx),函数f(x)=2
),sinx),函数f(x)=2 ![]()
![]() ,g(x)=f(
,g(x)=f( ![]() ).
).
(1)求f(x)在[ ![]() ,π]上的最值,并求出相应的x的值;
,π]上的最值,并求出相应的x的值;
(2)计算g(1)+g(2)+g(3)+…+g(2014)的值;
(3)已知t∈R,讨论g(x)在[t,t+2]上零点的个数.
【答案】
(1)解:f(x)=2 ![]()
![]() =2sinxsin(x﹣
=2sinxsin(x﹣ ![]() )+2sinxcosx=
)+2sinxcosx= ![]() sin2x+
sin2x+ ![]() sin2x
sin2x
= ![]() sin2x﹣
sin2x﹣ ![]() cos2x+
cos2x+ ![]() =sin(2x﹣
=sin(2x﹣ ![]() )+
)+ ![]() ,
,
∵x∈[ ![]() ,π],∴
,π],∴ ![]() ≤2x﹣
≤2x﹣ ![]() ≤
≤ ![]() ,
,
∴﹣1≤sin(2x﹣ ![]() )≤
)≤ ![]() ,f(x)最小值为
,f(x)最小值为 ![]() ﹣1,f(x)最大值为
﹣1,f(x)最大值为 ![]()
(2)解:由(1)得,f(x)=sin(2x﹣ ![]() )+
)+ ![]() .∴g(x)=f(
.∴g(x)=f( ![]() )=sin(
)=sin( ![]() x﹣
x﹣ ![]() )+
)+ ![]() .T=4,
.T=4,
∴g(1)+g(2)+g(3)+g(4)=g(5)+g(6)+g(7)+g(8)=…=g(2009)+g(2010)+g(2011)+g(2012).
g(1)+g(2)+g(3)+g(4)=2 ![]() ,g(1)+g(2)+g(3)+…+g(2014)=503×2
,g(1)+g(2)+g(3)+…+g(2014)=503×2 ![]() +
+
g(1)+g(2)
=1006 ![]() +
+ ![]() =
= ![]()
(3)解:g(x)在[t,t+2]上零点的个数等价于y=sin( ![]() x﹣
x﹣ ![]() )与y=﹣
)与y=﹣ ![]() 两图象交点个数.
两图象交点个数.
在同一直角坐标系内作出这两个数的图象.
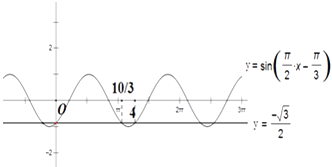
当4k<t< ![]() +4k,k∈Z时,由图象可知,y=sin(
+4k,k∈Z时,由图象可知,y=sin( ![]() x﹣
x﹣ ![]() )与y=﹣
)与y=﹣ ![]() 两图象无交点,g(x)无零点
两图象无交点,g(x)无零点
当 ![]() +4k≤t<2+4k或
+4k≤t<2+4k或 ![]() +4k<t≤4+4k时,y=sin(
+4k<t≤4+4k时,y=sin( ![]() x﹣
x﹣ ![]() )与y=﹣
)与y=﹣ ![]() 两图象1个交点,g(x)1个零点
两图象1个交点,g(x)1个零点
当2+4k≤t≤ ![]() +4k时,y=sin(
+4k时,y=sin( ![]() x﹣
x﹣ ![]() )与y=﹣
)与y=﹣ ![]() 两图象2个交点,g(x)2个零点
两图象2个交点,g(x)2个零点
【解析】(1)利用向量数量积的坐标运算,再利用三角函数公式化f(x)为含一个角的一种三角函数形式,利用三角函数的性质求最值.(2)由(1)得,g(x)=f( ![]() )=sin(
)=sin( ![]() x﹣
x﹣ ![]() )+
)+ ![]() .注意到T=4,利用分组方法求和.(3)g(x)在[t,t+2]上零点的个数等价于y=sin(
.注意到T=4,利用分组方法求和.(3)g(x)在[t,t+2]上零点的个数等价于y=sin( ![]() x﹣
x﹣ ![]() )与y=﹣
)与y=﹣ ![]() 两图象交点个数.利用数形结合的方法进行讨论.
两图象交点个数.利用数形结合的方法进行讨论.


科目:高中数学 来源: 题型:
【题目】已知,a,b,c分别是△ABC三个内角A,B,C的对边,下列四个命题:
①若tanA+tanB+tanC>0,则△ABC是锐角三角形
②若acoA=bcosB,则△ABC是等腰三角形
③若bcosC+ccosB=b,则△ABC是等腰三角形
④若 ![]() =
= ![]() ,则△ABC是等边三角形
,则△ABC是等边三角形
其中正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体ABCD﹣A′B′C′D′. 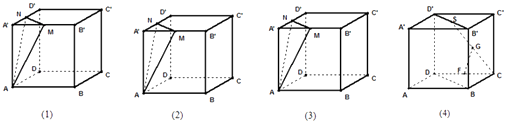
(1)设M,N分别是A′D′,A′B′的中点,试在下列三个正方体中各作出一个过正方体顶点且与平面AMN平行的平面(不用写过程)
(2)设S是B′D′的中点,F,G分别是DC,SC的中点,求证:直线GF∥平面BDD′B′.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx+c.
(1)若f(﹣1)=0,f(0)=0,求出函数f(x)的零点;
(2)若f(x)同时满足下列条件:①当x=﹣1时,函数f(x)有最小值0,②f(1)=1求函数f(x)的解析式;
(3)若f(1)≠f(3),证明方程f(x)= ![]() [f(1)+f(3)]必有一个实数根属于区间(1,3)
[f(1)+f(3)]必有一个实数根属于区间(1,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() ,
,![]() ,
,![]() 为
为![]() 中点.
中点.
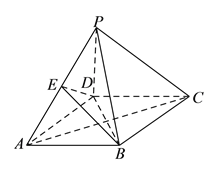
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 的交点记为
的交点记为![]() ,求证
,求证![]() 平面
平面![]() ;
;
(3)在(2)的条件下求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)
已知椭圆![]() 的短轴长为
的短轴长为![]() ,且与抛物线
,且与抛物线![]() 有共同的焦点,椭圆
有共同的焦点,椭圆![]() 的左顶点为A,右顶点为
的左顶点为A,右顶点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上位于
上位于![]() 轴上方的动点,直线
轴上方的动点,直线![]() ,
,![]() 与直线
与直线![]() 分别交于
分别交于![]() 两点.
两点.
(I)求椭圆![]() 的方程;
的方程;
(Ⅱ)求线段![]() 的长度的最小值;
的长度的最小值;
(Ⅲ)在线段![]() 的长度取得最小值时,椭圆
的长度取得最小值时,椭圆![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 的面积为
的面积为![]() ,若存在求出点
,若存在求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入![]() 万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从![]() 开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入![]() 万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 2 | 7 |
由表中的数据显示, ![]() 与
与![]() 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出![]() 关于
关于![]() 的回归直线方程.
的回归直线方程.
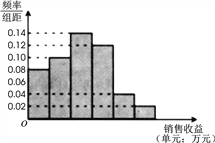
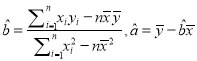
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市从现有甲、乙两种酸奶的日销售量(单位:箱)的1200个数据(数据均在区间![]() 内)中,按照5%的比例进行分层抽样,统计结果按
内)中,按照5%的比例进行分层抽样,统计结果按![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组,整理如下图:
分组,整理如下图:
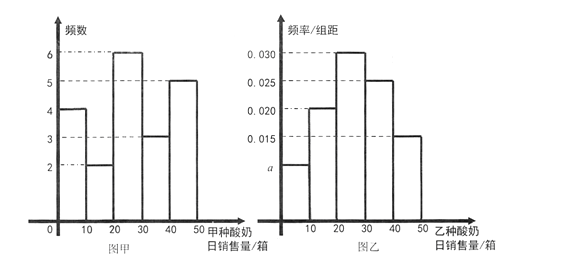
(Ⅰ)写出频率分布直方图(图乙)中![]() 的值;记所抽取样本中甲种酸奶与乙种酸奶日销售量的方差分别为
的值;记所抽取样本中甲种酸奶与乙种酸奶日销售量的方差分别为![]() ,
, ![]() ,试比较
,试比较![]() 与
与![]() 的大小(只需写出结论);
的大小(只需写出结论);
(Ⅱ)从甲种酸奶日销售量在区间![]() 的数据样本中抽取3个,记在
的数据样本中抽取3个,记在![]() 内的数据个数为
内的数据个数为![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)估计1200个日销售量数据中,数据在区间![]() 中的个数.
中的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中, ![]() ,点E,H分别是所在边靠近B,D的三等分点,现沿着EH将矩形折成直二面角,分别连接AD,AC,CB,形成如图所示的多面体.
,点E,H分别是所在边靠近B,D的三等分点,现沿着EH将矩形折成直二面角,分别连接AD,AC,CB,形成如图所示的多面体.
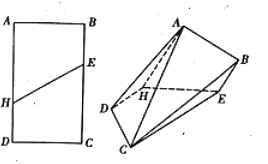
(1)证明:平面BCE∥平面ADH;
(2)证明:EH⊥AC;
(3)求二面角B-AC-D的平面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com