
已知抛物线 的焦点为F2,点F1与F2关于坐标原点对称,直线m垂直于x轴(垂足为T),与抛物线交于不同的两点P,Q且
的焦点为F2,点F1与F2关于坐标原点对称,直线m垂直于x轴(垂足为T),与抛物线交于不同的两点P,Q且 .
.
(I)求点T的横坐标 ;
;
(II)若以F1,F2为焦点的椭圆C过点 .
.
①求椭圆C的标准方程;
②过点F2作直线l与椭圆C交于A,B两点,设 ,若
,若 的取值范围.
的取值范围.
(I) ;(II)①
;(II)①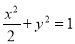 ,②
,②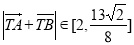
【解析】
试题分析:(Ⅰ)由题意得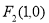 ,
,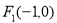 ,设
,设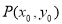 ,
,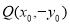 ,由已知
,由已知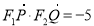 得到关于
得到关于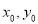 的一个方程
的一个方程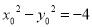 ;又点
;又点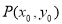 在抛物线上得方程
在抛物线上得方程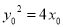 ,联立方程解得
,联立方程解得 ;(II)①由已知得椭圆的半焦距
;(II)①由已知得椭圆的半焦距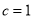 ,设椭圆
,设椭圆 的标准方程为
的标准方程为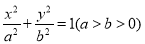 ,由椭圆过点
,由椭圆过点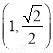 可得
可得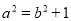 ,又
,又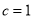 即
即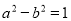 ,从而解得
,从而解得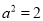 ,
,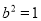 ;②容易验证直线
;②容易验证直线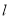 的斜率不为0,设直线
的斜率不为0,设直线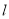 的方程为
的方程为 ,将直线方程代入椭圆方程得
,将直线方程代入椭圆方程得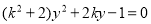 ,设
,设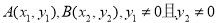 ,利用根与系数的关系得
,利用根与系数的关系得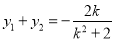 ,
,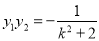 ,因为
,因为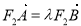 ,所以
,所以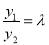 ,且
,且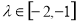 将和平方除以积化简得
将和平方除以积化简得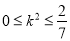 ,将所求的模平方通过坐标运算转化为关于k 的函数,解得
,将所求的模平方通过坐标运算转化为关于k 的函数,解得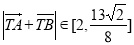 。
。
试题解析:(Ⅰ)由题意得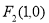 ,
,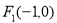 ,设
,设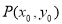 ,
,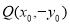 ,
,
则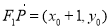 ,
, .
.
由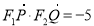 ,得
,得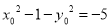 即
即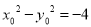 ,①
,①
又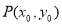 在抛物线上,则
在抛物线上,则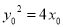 ,②
,②
联立①、②易得
(Ⅱ)(ⅰ)设椭圆的半焦距为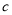 ,由题意得
,由题意得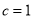 ,
,
设椭圆 的标准方程为
的标准方程为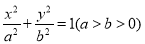 ,则
,则 ③
③
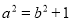 ④
④
将④代入③,解得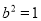 或
或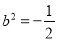 (舍去)
(舍去)
所以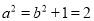
故椭圆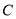 的标准方程为
的标准方程为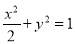
(ⅱ)方法一:
容易验证直线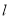 的斜率不为0,设直线
的斜率不为0,设直线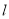 的方程为
的方程为 ,
,
将直线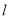 的方程代入
的方程代入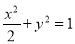 中得:
中得: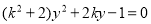
设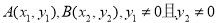 ,则由根与系数的关系,
,则由根与系数的关系,
可得: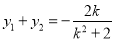 ⑤
⑤
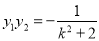 ⑥
⑥
因为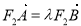 ,所以
,所以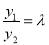 ,且
,且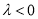 .
.
将⑤式平方除以⑥式,得:
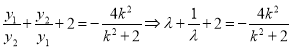
由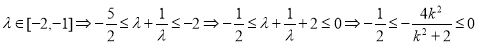
所以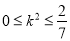 。
。
因为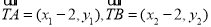 ,所以
,所以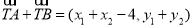 ,
,
又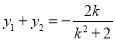 ,所以
,所以 ,
,
故
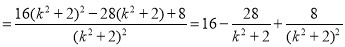 ,
,
令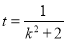 ,所以
,所以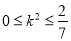 所以
所以 ,即
,即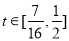 ,
,
所以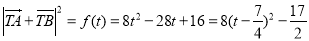 .
.
而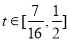 ,所以
,所以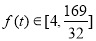 .
.
所以 .
.
方法二:
1)当直线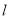 的斜率不存在时,即
的斜率不存在时,即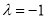 时,
时,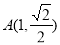 ,
,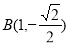
又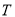
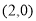 ,所以
,所以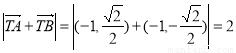
2)当直线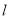 的斜率存在时,即
的斜率存在时,即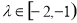 时,设直线
时,设直线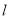 的方程为
的方程为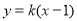
由 得
得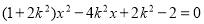
设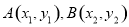 ,显然
,显然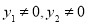 ,则由根与系数的关系,
,则由根与系数的关系,
可得: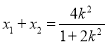 ,
,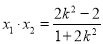
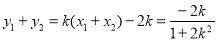 ⑤
⑤
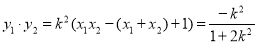 ⑥
⑥
因为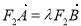 ,所以
,所以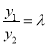 ,且
,且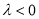 .
.
将⑤式平方除以⑥式得:
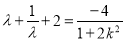
由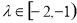 得
得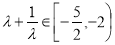 即
即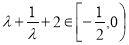
故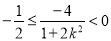 ,解得
,解得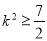
因为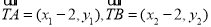 ,
,
所以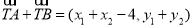 ,
,
又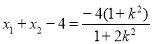 ,
,
故
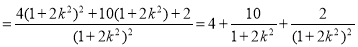
令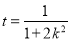 ,因为
,因为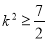 所以
所以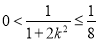 ,即
,即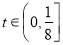 ,
,
所以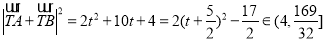 .
.
所以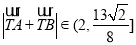
综上所述: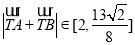 .
.
考点:圆锥曲线定义与性质以及平面解释几何的综合应用。


科目:高中数学 来源:2015届山东省高二暑假作业二数学试卷(解析版) 题型:选择题
点 到图形
到图形 上每一个点的距离的最小值称为点
上每一个点的距离的最小值称为点 到图形
到图形 的距离,那么平面内到定圆
的距离,那么平面内到定圆 的距离与到定点
的距离与到定点 的距离相等的点的轨迹不可能是( )
的距离相等的点的轨迹不可能是( )
A.圆 B.椭圆 C.双曲线的一支 D.直线
查看答案和解析>>
科目:高中数学 来源:2015届山东省菏泽市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
某班有60名学生,一次考试后数学成绩ξ~N(110,102),若P(100≤ξ≤110)=0.35,则估计该班学生数学成绩在120分以上的人数为( ).
A.10 B.9 C.8 D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com