
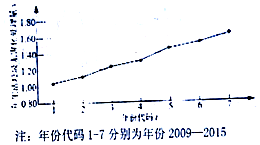
 如图是我国2009年至2015年生活垃圾无害化处理量(单位:亿吨)的折线图
如图是我国2009年至2015年生活垃圾无害化处理量(单位:亿吨)的折线图分析 (1)求出变量y与t的相关系数,可得结论;
(2)求出回归系数,可得回归方程,即可预测2017年我国生活垃圾无害化处理1.83亿吨.
解答 解:(1)变量y与t的相关系数r=$\frac{7×40.17-28×9.32}{7×5.292×0.55}$≈0.99,….(5分)
故可用线性回归模型拟合变量y与t的关系.…..(6分)
(2)$\overline{t}$=4,$\overline{y}$=$\frac{1}{7}$$\sum_{i=1}^{7}$yi,所以$\stackrel{∧}{b}$=$\frac{40.17-7×4×\frac{1}{7}×9.32}{28}$=0.1,
$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$t=$\frac{1}{7}×9.32-0.10×4≈0.93$,…..(10分)
所以线性回归方程为$\stackrel{∧}{y}$=0.1t+0.93,
当t=9时,$\stackrel{∧}{y}$=0.1×9+0.93=1.83,
因此,我们可以预测2017年我国生活垃圾无害化处理1.83亿吨 …(12分)
点评 本题考查回归方程,考查学生的计算能力,属于中档题.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,+∞) | B. | (-1,-$\frac{2}{3}$) | C. | (3,+∞) | D. | (-$\frac{2}{3}$,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 常喝 | 不常喝 | 合计 | |
| 肥胖 | 60 | ||
| 不肥胖 | 10 | ||
| 合计 | 100 |
| P(x2≥x0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| x0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$与$\overrightarrow{b}$为平行向量 | B. | $\overrightarrow{a}$与$\overrightarrow{b}$为模相等的向量 | ||
| C. | $\overrightarrow{a}$与$\overrightarrow{b}$为共线向量 | D. | $\overrightarrow{a}$与$\overrightarrow{b}$为相等的向量 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com