
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 由题意,使$|{\overrightarrow{OA}-\overrightarrow{OB}}|≤1$成立时,0°≤∠AOB≤60°,即可求出在圆O上随机取一点B,使$|{\overrightarrow{OA}-\overrightarrow{OB}}|≤1$成立的概率.
解答 解:由题意,使$|{\overrightarrow{OA}-\overrightarrow{OB}}|≤1$成立时,0°≤∠AOB≤60°,
∴在圆O上随机取一点B,则使$|{\overrightarrow{OA}-\overrightarrow{OB}}|≤1$成立的概率为$\frac{120}{360}$=$\frac{1}{3}$,
故选B.
点评 本题考查几何概型,考查向量知识的运用,正确求出角度是关键.


科目:高中数学 来源: 题型:解答题
 共享单车的出现方便了人们的出行,深受我市居民的喜爱.为调查某校大学生对共享单车的使用情况,从该校8000名学生中按年级用分层抽样的方式随机抽取了100位同学进行调查,得到这100名同学每周使用共享单车的时间(单位:小时)如表:
共享单车的出现方便了人们的出行,深受我市居民的喜爱.为调查某校大学生对共享单车的使用情况,从该校8000名学生中按年级用分层抽样的方式随机抽取了100位同学进行调查,得到这100名同学每周使用共享单车的时间(单位:小时)如表:| 使用时间 | [0,2] | (2,4] | (4,6] | (6,8] | (8,10] |
| 人数 | 10 | 40 | 25 | 20 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,M为AD上的点,AE=1,AM=$\frac{1}{2}$.
边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,M为AD上的点,AE=1,AM=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 年薪(万元) | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2和1 | B. | 2和0 | C. | 2和-1 | D. | 2和-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2-2x-4 | B. | x2+x-1 | C. | x2+2x | D. | x2-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
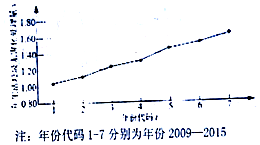 如图是我国2009年至2015年生活垃圾无害化处理量(单位:亿吨)的折线图
如图是我国2009年至2015年生活垃圾无害化处理量(单位:亿吨)的折线图查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com