
已知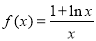 .
.
(1)求函数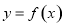 的单调区间;
的单调区间;
(2)若关于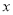 的方程
的方程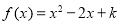 有实数解,求实数
有实数解,求实数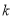 的取值范围;
的取值范围;
(3)当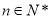 ,
,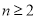 时,求证:
时,求证: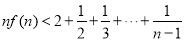 .
.
(1)函数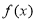 在区间(0,1)上为增函数;在区间
在区间(0,1)上为增函数;在区间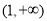 为减函数;(2)
为减函数;(2)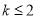 ;(3)详见解析.
;(3)详见解析.
【解析】
试题分析:(Ⅰ)先求出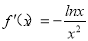 ,从而得函数f(x)在区间(0,1)上为增函数;在区间(1,+∞)为减函数.(Ⅱ)由(Ⅰ)得f(x)的极大值为f(1)=1,令
,从而得函数f(x)在区间(0,1)上为增函数;在区间(1,+∞)为减函数.(Ⅱ)由(Ⅰ)得f(x)的极大值为f(1)=1,令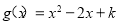 ,得函数 g(x)取得最小值g(1)=k-1,由
,得函数 g(x)取得最小值g(1)=k-1,由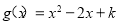 有实数解,k-1≤1,进而得实数k的取值范围.(Ⅲ)由
有实数解,k-1≤1,进而得实数k的取值范围.(Ⅲ)由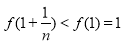 ,得
,得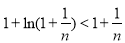 ,从而
,从而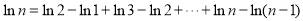
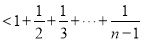 ,即
,即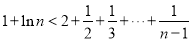 ,问题得以解决.
,问题得以解决.
试题解析:解:(1)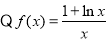 ,∴
,∴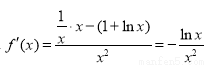
∴当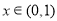 时,
时,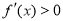 ;当
;当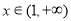 时,
时,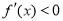 ;
;
∴函数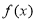 在区间(0,1)上为增函数;在区间
在区间(0,1)上为增函数;在区间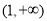 为减函数 4分
为减函数 4分
(2)由(1)得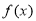 的极大值为
的极大值为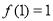 ,令
,令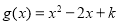 ,
,
所以当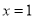 时,函数
时,函数 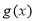 取得最小值
取得最小值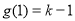 ,
,
又因为方程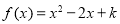 有实数解,那么
有实数解,那么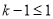 , 即
, 即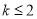 ,
,
所以实数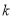 的取值范围是:
的取值范围是: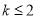 . 8分
. 8分
(3)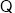 函数
函数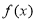 在区间
在区间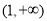 为减函数,而
为减函数,而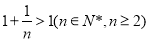 ,
,
∴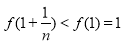 ∴
∴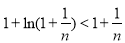 ,即
,即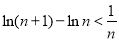
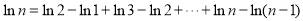
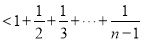
即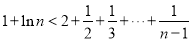 ,而
,而 ,
,
∴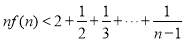 结论成立. 12分.
结论成立. 12分.
考点:1.利用导数研究函数的单调性;2.导数在最大值、最小值问题中的应用.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源:2015届福建省八县(市高三上学期半期联考文科数学试卷(解析版) 题型:选择题
函数f(x)=sin(ωx+φ),(其中|φ|< )的图象如图所示,为了得到g(x)=sinωx的图象,则只要将f(x)的图象( )
)的图象如图所示,为了得到g(x)=sinωx的图象,则只要将f(x)的图象( )

A.向右平移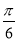 个单位 B.向右平移
个单位 B.向右平移 个单位
个单位
C.向左平移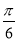 个单位 D.向左平移
个单位 D.向左平移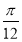 个单位
个单位
查看答案和解析>>
科目:高中数学 来源:2015届甘肃省高三第一次诊断考试理科数学试卷(解析版) 题型:选择题
设 是定义在R上的偶函数,且在
是定义在R上的偶函数,且在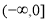 上是增函数 ,
上是增函数 ,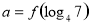 ,
, ,
, ,则
,则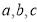 的大小关系是( )
的大小关系是( )
A.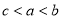 B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届甘肃省高二下学期模块检测理科数学试卷(解析版) 题型:解答题
某高校在2014年自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩较高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
(ⅰ)已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙恰有一人进入第二轮面试的概率;
(ⅱ)学校决定在这已抽取到的6名学生中随机抽取2名学生接受考官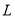 的面试,设第4组中有
的面试,设第4组中有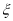 名学生被考官
名学生被考官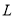 面试,求
面试,求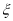 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
科目:高中数学 来源:2015届湖南省衡阳市高三上学期五校联考理科数学试卷(解析版) 题型:选择题
已知 是非空集合,命题甲:
是非空集合,命题甲: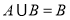 ,命题乙:
,命题乙: ,那么( )
,那么( )
A.甲是乙的充分不必要条件
B.甲是乙的必要不充分条件
C.甲是乙的充要条件
D.甲是乙的既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com