Question

15．方程lgx=2-x精确度0.1的近似根a≈1.8125；用a表示方程10^x=2-x的一个根x=2-a．

Answer 1

分析 作出y=lg x，y=2-x的图象，可以发现，方程lg x=2-x有唯一解，记为x₀，并且解在区间（1，2）内．利用函数零点的判定定理即可得出．由于y=lgx与y=10^x互为反函数，可得方程10^x=2-x的一个根．

解答 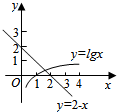解：作出y=lg x，y=2-x的图象，可以发现，方程lg x=2-x有唯一解，记为x₀，并且解在区间（1，2）内．
设f（x）=lg x+x-2，用计算器计算
得f（1）＜0，f（2）＞0⇒x₀∈（1，2）；
f（1.5）＜0，f（2）＞0⇒x₀∈（1.5，2）；
f（1.75）＜0，f（2）＞0⇒x₀∈（1.75，2）；
f（1.75）＜0，f（1.875）＞0⇒x₀∈（1.75，1.875）；
f（1.75）＜0，f（1.812 5 ）＞0⇒x₀∈（1.75，1.812 5）；
∵|1.812 5-1.75|=0.062 5＜0.1，
∴a≈1.812 5；
由y=x与y=2-x联立，可得x=y=1，由于y=lgx与y=10^x互为反函数，可得方程10^x=2-x的一个根x=2-a．
故答案为：1.812 5；2-a．

点评 熟练掌握函数零点的判定定理及二分法求函数零点的方法、数形结合思想是解题的关键．