
| A. | $\frac{2}{5}$ | B. | $\frac{7}{20}$ | C. | $\frac{9}{25}$ | D. | $\frac{11}{25}$ |
分析 先求出基本事件总数n=${A}_{5}^{1}$•${A}_{5}^{2}$,再求出该三位数能被5整除包含的基本事件个数m=${A}_{5}^{2}$+C${\;}_{4}^{1}$A${\;}_{4}^{1}$,由此能求出该三位数能被5整除的概率.
解答 解:从由数字0,1,2,3,4,5组成的没有重复数字的所有三位数中任取一个,
基本事件总数n=${A}_{5}^{1}$•${A}_{5}^{2}$=100,
该三位数能被5整除包含的基本事件个数m=${A}_{5}^{2}$+C${\;}_{4}^{1}$A${\;}_{4}^{1}$=36,
∴该三位数能被5整除的概率为p=$\frac{m}{n}$=$\frac{36}{100}$=$\frac{9}{25}$.
故选:C.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,点E、F分别为棱长为2$\sqrt{2}$的正方体ABCD-A1B1C1D1的棱AB,C1D1的中点,点P在EF上,过点P作直线l,使得l⊥EF,且l∥平面ACD1,直线l与正方体的表面相交于M、N两点,当点P由E运动到点F时,记EP=x,△EMN的面积为f(x),则y=f(x)的图象是( )
如图所示,点E、F分别为棱长为2$\sqrt{2}$的正方体ABCD-A1B1C1D1的棱AB,C1D1的中点,点P在EF上,过点P作直线l,使得l⊥EF,且l∥平面ACD1,直线l与正方体的表面相交于M、N两点,当点P由E运动到点F时,记EP=x,△EMN的面积为f(x),则y=f(x)的图象是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
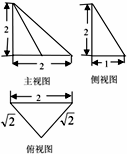
| A. | 1+$\sqrt{2}$+$\sqrt{3}$ | B. | 2+$\sqrt{2}$+$\sqrt{3}$ | C. | 3+$\sqrt{2}$+$\sqrt{3}$ | D. | 4+$\sqrt{2}$+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com