
| A. | $\frac{\sqrt{5}}{6}$ | B. | $\frac{\sqrt{13}}{4}$ | C. | $\frac{\sqrt{2}}{10}$ | D. | $\frac{\sqrt{3}}{5}$ |
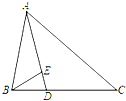
分析 解法一:由条件利用两个向量的加减法的法则,以及其几何意义求得$\overrightarrow{BD}$、$\overrightarrow{AD}$、$\overrightarrow{AE}$,可得$\overrightarrow{BE}$,再利用两个向量数量积的定义,求得|$\overrightarrow{BE}$|的值.
解法二:延长BE交AC于点F,作DG∥BF,交AC于点G,设AF=3m,EF=3n,由三角形相似求得m、n的值,可得BE=$\frac{BF}{2}$的值.
解答 解:在△ABC中,已知∠BAC=$\frac{π}{3}$,AB=2,AC=3,$\overrightarrow{DC}$=2$\overrightarrow{BD}$,$\overrightarrow{AE}$=3$\overrightarrow{ED}$,
∴$\overrightarrow{BD}$=$\frac{1}{3}$$\overrightarrow{BC}$=$\frac{\overrightarrow{AC}-\overrightarrow{AB}}{3}$,$\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BD}$=$\overrightarrow{AB}$+$\frac{1}{3}\overrightarrow{BC}$=$\overrightarrow{AB}$+$\frac{1}{3}$($\overrightarrow{AC}$-$\overrightarrow{AB}$)
=$\frac{2\overrightarrow{AB}}{3}$+$\frac{\overrightarrow{AC}}{3}$,$\overrightarrow{AE}$=$\frac{3}{4}$$\overrightarrow{AD}$=$\frac{3}{4}$•($\frac{2\overrightarrow{AB}}{3}$+$\frac{\overrightarrow{AC}}{3}$)=$\frac{2\overrightarrow{AB}+\overrightarrow{AC}}{4}$,
∴$\overrightarrow{BE}$=$\overrightarrow{AE}$-$\overrightarrow{AB}$=$\frac{2\overrightarrow{AB}+\overrightarrow{AC}}{4}$-$\overrightarrow{AB}$=$\frac{\overrightarrow{AC}-2\overrightarrow{AB}}{4}$,
故 ${\overrightarrow{BE}}^{2}$=$\frac{1}{16}$(${\overrightarrow{AC}}^{2}$+4${\overrightarrow{AB}}^{2}$-4$\overrightarrow{AB}•\overrightarrow{AC}$ )=$\frac{1}{16}$(9+16-4•2•3•cos$\frac{π}{3}$)=$\frac{13}{16}$,
∴|$\overrightarrow{BE}$|=$\frac{\sqrt{13}}{4}$,
故选:B.
解法二:如图:在△ABC中,已知∠BAC=$\frac{π}{3}$,AB=2,AC=3,$\overrightarrow{DC}$=2$\overrightarrow{BD}$,$\overrightarrow{AE}$=3$\overrightarrow{ED}$,
延长BE交AC于点F,作DG∥BF,交AC于点G,设AF=3m,EF=3n,
由△AEF∽△ADG,可得$\frac{EF}{DG}$=$\frac{AE}{AD}$=$\frac{AF}{AG}$,即$\frac{3n}{DG}$=$\frac{3}{4}$=$\frac{3m}{AG}$,
∴DG=4n,AG=4m,∴FG=m.
由△CDG∽△CBF可得$\frac{DG}{BF}=\frac{CD}{CB}$=$\frac{CG}{CF}$,即$\frac{4n}{BF}$=$\frac{2}{3}$=$\frac{CG}{3-3m}$,
∴BF=6n,CG=2-2m,∴BE=BF-EF=3n,根据AC=AF+FG+GC=3m+m+2-2m=3,∴m=$\frac{1}{2}$.
即F为AC的中点,AF=$\frac{3}{2}$,E为BF的中点.
△ABF中,有余弦定理可得BF2=(6n)2=AB2+AF2-2AB•AF•cos∠BAC=4+${(\frac{3}{2})}^{2}$-2•2•$\frac{3}{2}$•$\frac{1}{2}$,
∴9n2=$\frac{13}{16}$,∴BE=$\sqrt{{9n}^{2}}$=$\frac{\sqrt{13}}{4}$.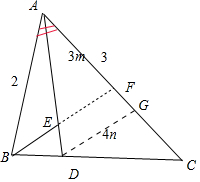
点评 本题主要考查两个向量的加减法的法则,以及其几何意义,求向量的模的方法,两个向量数量积的定义;三角形相似,余弦定理,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
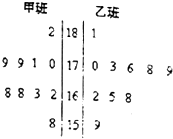 随机抽取某中学甲乙两班10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.
随机抽取某中学甲乙两班10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | 2 | C. | 3 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -1 | C. | -5 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com