
分析 ①先化简函数f(x),求函数的导数f′(x),得到f′(x)=0的根有无数个,
②函数为偶函数,
③判断函数f(x)存在大于0的实数,
④根据函数的周期性进行判断.
解答 解:f(x)=2xsin$\frac{x}{2}$cos$\frac{x}{2}$=xsinx,则函数f(x)为偶函数,
函数的导数f′(x)=sinx+xcosx,
由f′(x)=0得sinx+xcosx=0,得sinx=-xcosx,当cosx=0时,sinx=±1,此时方程无解,
则cosx≠0,即tanx=-x,此时方程tanx=-x有无数多个解,则函数y=f(x)由无数多个极值点,故①正确,
∵f(x)=xsinx为偶函数,∴?x∈R,都有f(-x)=f(x)成立,故②错误,
当x>0,且sinx>0时,f(x)=xsinx>0,则③?M>0,至少存在一个实数x0,使得f(x0)>M成立,故③正确,
函数f(x)不是周期函数,故?x∈R,恒有f(x+T)=f(x)不成立,故④错误,
故答案为:①③
点评 本题主要考查命题的真假判断,涉及函数的奇偶性,极值,周期性以及取值,考查学生的推理能力.


科目:高中数学 来源: 题型:选择题
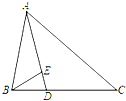
| A. | $\frac{\sqrt{5}}{6}$ | B. | $\frac{\sqrt{13}}{4}$ | C. | $\frac{\sqrt{2}}{10}$ | D. | $\frac{\sqrt{3}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${(x-1)^2}+{y^2}=\frac{36}{25}$ | B. | ${x^2}+{(y-1)^2}=\frac{36}{25}$ | C. | (x-1)2+y2=1 | D. | x2+(y-1)2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
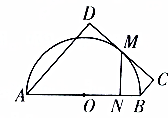 如图:已知AB为圆O的直径,直线CD与圆O相切与M,AD⊥CD于D,BC⊥CD于C,MN⊥AB于N,AD=3,BC=1.
如图:已知AB为圆O的直径,直线CD与圆O相切与M,AD⊥CD于D,BC⊥CD于C,MN⊥AB于N,AD=3,BC=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com