
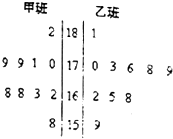
 随机抽取某中学甲乙两班10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.
随机抽取某中学甲乙两班10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.分析 (1)观察茎叶图,得到乙班平均身高高于甲班.
(2)利用列举法能得到抽取学生的所有不同的抽取结果.
(3)利用列举法能求出抽取两人中甲班身高不低于乙班同学身高的概率.
解答 解:(1)由茎叶图可知:
甲班身高集中于160~169之间,而乙班身高集中于170~180之间,
因此乙班平均身高高于甲班.
(2)由列举法得抽取学生的所有不同的抽取结果为:
(179,173),(179,176),(179,178),(179,179),(179,181),
(182,173),(182,176),(182,178),(182,179),(182,181).
(3)由(2)知基本事件总数n=10,
抽取两人中甲班身高不低于乙班同学身高包含的基本事件有:
(179,173),(179,176),(179,178),(179,179),(182,173),
(182,176),(182,178),(182,179),(182,181),共有9个,
∴抽取两人中甲班身高不低于乙班同学身高的概率p=$\frac{9}{10}$.
点评 本题考查平均身高的比较,考查概率的求法,是基础题,解题时要认真审题,注意列举法和茎叶图性质的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|$\frac{π}{2}$<x<π} | B. | {x|$\frac{π}{2}$<x<$\frac{3}{2}$π} | C. | {x|$\frac{π}{2}$<x<2π} | D. | {x|0<x<$\frac{π}{2}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{{{x^2}+1}}<1$ | B. | x2+1≥2|x| | C. | lg(x2+1)≥lg2x | D. | $\frac{4x}{{{x^2}+4}}$≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [1,+∞) | C. | (-∞,-1] | D. | (-∞,-1]∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{6}$ | B. | $\frac{\sqrt{13}}{4}$ | C. | $\frac{\sqrt{2}}{10}$ | D. | $\frac{\sqrt{3}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${(x-1)^2}+{y^2}=\frac{36}{25}$ | B. | ${x^2}+{(y-1)^2}=\frac{36}{25}$ | C. | (x-1)2+y2=1 | D. | x2+(y-1)2=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com