
分析 由条件可得z=3-2x+3y,x2+(y-1)2+z2=x2+(y-1)2+(3-2x+3y)2,配方由非负数概念,可得最小值和y的值.
解答 解:z=3-2x+3y,
x2+(y-1)2+z2=x2+(y-1)2+(3-2x+3y)2=5x2-12x(y+1)+9(y+1)2+(y-1)2
=5[x-1.2(y+1)]2+1.8(y+1)2+(y-1)2
=5[x-1.2(y+1)]2+2.8y2+1.6y+2.8
=5[x-1.2(y+1)]2+2.8[y2+$\frac{1.6}{2.8}$y+($\frac{0.8}{2.8}$)2]+2.8-$\frac{0.{8}^{2}}{2.8}$
=5[x-1.2(y+1)]2+2.8(y+$\frac{2}{7}$)2+$\frac{18}{7}$≥$\frac{18}{7}$.
当且仅当x=$\frac{6}{7}$,y=-$\frac{2}{7}$时,取得最小值,且为$\frac{18}{7}$.
故答案为:$\frac{18}{7}$,-$\frac{2}{7}$.
点评 本题考查最小值的求法,注意运用配方法和非负数的思想,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “x<1”是“x2-3x+2>0”的必要不充分条件 | |
| B. | 命题“若x2-3x+2=0,则x=2”的否命题为“若x2-3x+2=0,则x≠2 | |
| C. | 若p∧q为假命题,则p,q均为假命题 | |
| D. | 对于命题p:?x∈R,使得x2+x-1<0,则?p:?x∈R,均有x2+x-1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{\sqrt{7}}{4}$ | D. | -$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
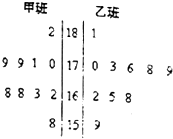 随机抽取某中学甲乙两班10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.
随机抽取某中学甲乙两班10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 669 | B. | 670 | C. | 2008 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com