
分析 实数a,b,c,d满足(a-lnb)2+(c-d)2=0,可得a=lnb,c=d.令y=f(x)=lnx,y=g(x)=x,转化为求上述两曲线之间的最小距离,设直线y=x+m与曲线f(x)=lnx相切于点P(x0,y0).利用导数的几何意义求出切点,进而得出.
解答 解:实数a,b,c,d满足(a-lnb)2+(c-d)2=0,∴a=lnb,c=d.
令y=f(x)=lnx,y=g(x)=x,
设直线y=x+m与曲线f(x)=lnx相切于点P(x0,y0).
f′(x)=$\frac{1}{x}$,∴$\frac{1}{{x}_{0}}$=1,解得x0=1,可得P(1,0),
代入切线方程可得:0=1+m,解得m=-1.
则两条平行线y=x,y=x-1的距离d=$\frac{1}{\sqrt{2}}$.
∴(a-c)2+(b-d)2的最小值为d2=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了导数的几何意义、两点之间的距离公式、点到直线的距离公式、平行线之间的距离公式、等价转化方法,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
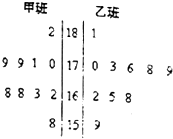 随机抽取某中学甲乙两班10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.
随机抽取某中学甲乙两班10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | 2 | C. | 3 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -1 | C. | -5 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 3 | C. | 6 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com