练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数f(x)＝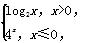

    则f(f(－1))＝________；若函数g(x)＝f(x)－k存在两个零点，则实数k的取值范围是________．


    －2　(0,1]

    [解析]　f(f(－1))＝f(4－1)＝f＝log2＝－2.令f(x)－k＝0，即f(x)＝k，设y＝f(x)，y＝k，画出图象，如图所示，函数g(x)＝f(x)－k存在两个零点，即y＝f(x)与y＝k的图象有两个交点，由图象可得实数k的取值范围为(0,1]．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    在实验室进行的一项物理实验中，要先后实施6个程序，其中程序A只能出现在第一或最后一步，程序B和C在实施时必须相邻，则实验顺序的编排方法共有(　　)

    A．34种  B．48种  C．96种  D．144种

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知t>－1，当x∈[－t，t＋2]时，函数y＝(x－4)|x|的最小值为－4，则t的取值范围________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知g(x)＝－x2－4，f(x)为二次函数，满足f(x)＋g(x)＋f(－x)＋g(－x)＝0，且f(x)在[－1,2]上的最大值为7，则f(x)＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝

    是(－∞，＋∞)上的减函数，那么实数a的取值范围是(　　)

    A．(0,1)     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)为定义在R上的偶函数，当x≥0时，有f(x＋1)＝－f(x)，且当x∈[0,1)时，f(x)＝log2(x＋1)，给出下列命题：

    ①f(2 013)＋f(－2 014)的值为0；

    ②函数f(x)在定义域上为周期是2的周期函数；

    ③直线y＝x与函数f(x)的图象有1个交点；

    ④函数f(x)的值域为(－1,1)．

    其中正确命题的序号有________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，已知正方体ABCD－A1B1C1D1的棱长是1，点E是对角线AC1上一动点，记AE＝x(0<x<)，过点E平行于平面A1BD的截面将正方体分成两部分，其中点A所在的部分的体积为V(x)，则函数y＝V(x)的图象大致为(　　)

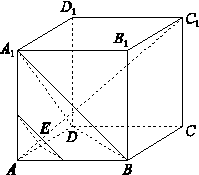
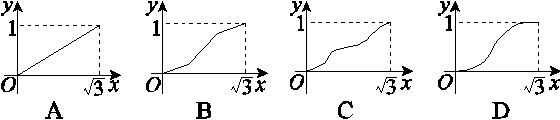
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a，b是两个互相垂直的单位向量，且c·a＝c·b＝1，则对任意的正实数t，的最小值是(　　)

    A．2  B．2  C．4  D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在不等边△ABC(三边均不相等)中，三个内角A，B，C所对的边分别为a，b，c，且有＝，则角C的大小为________．

    查看答案和解析>>

    同步练习册答案