
分析 (1)根据椭圆的离心率和右焦点F2与椭圆上点的连线的中最短线段的长,
列出方程组求出a、c的值,再求出b的值,即可写出椭圆Γ的标准方程;
(2)设点P、A和B的坐标,写出直线lPA的方程,并与椭圆方程组成方程组,
消去x,得关于y的一元二次方程,由根与系数的关系,
结合题意求出点P的坐标,即可求出直线PB的斜率值.
解答 解:(1)椭圆$Γ:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,
∴$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,…①
右焦点F2与椭圆上点的连线的中最短线段的长为$\sqrt{2}-1$,
即a-c=$\sqrt{2}$-1;…②
由①②解得a=$\sqrt{2}$,c=1,
∴b=$\sqrt{{a}^{2}{-c}^{2}}$=1;
∴椭圆Γ的标准方程是$\frac{{x}^{2}}{2}$+y2=1;
(2)设点P(x0,y0),A(x1,y1),B(x2,y2),
则直线lPA的方程为:x=my-1;
由$\left\{\begin{array}{l}{x=my-1}\\{{x}^{2}+{2y}^{2}=2}\end{array}\right.$,消去x,得(m2+1)y2-2my-1=0;
则y0•y1=-$\frac{1}{{m}^{2}+2}$,
又$\frac{1}{m}$=$\frac{{y}_{0}}{{x}_{0}+1}$,∴m=$\frac{{x}_{0}+1}{{y}_{0}}$;
∴$\frac{|{PF}_{1}|}{{|F}_{1}A|}$=-$\frac{{y}_{0}}{{y}_{1}}$=-$\frac{{y}_{0}}{-\frac{1}{{(m}^{2}+2{)y}_{0}}}$
=(m2+2)${{y}_{0}}^{2}$=[$\frac{{{(x}_{0}+1)}^{2}}{{{y}_{0}}^{2}}$+2]${{y}_{0}}^{2}$
=${{(x}_{0}+1)}^{2}$+2${{y}_{0}}^{2}$=${{(x}_{0}+1)}^{2}$+2-${{x}_{0}}^{2}$;
∴$\frac{|{PF}_{1}|}{{|F}_{1}A|}$=3+2x0,∴2+2x0=2,
解得x0=-$\frac{1}{2}$,
∴P(-$\frac{1}{2}$,±$\frac{\sqrt{14}}{4}$),
∴KPB=${K}_{{PF}_{2}}$=$\frac{±\frac{\sqrt{14}}{4}}{-\frac{1}{2}-1}$=$\overline{+}$$\frac{\sqrt{14}}{6}$;
故直线PB的斜率为±$\frac{\sqrt{14}}{6}$.
点评 本题考查了直线与圆锥曲线方程的综合应用问题,也考查了方程组和根与系数的应用问题,是综合性题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
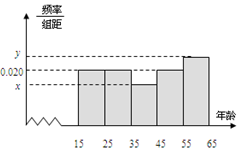 某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.
某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.| 组号 | 分组 | 喜爱人数 | 喜爱人数 占本组的频率 |
| 第1组 | [15,25) | a | 0.10 |
| 第2组 | [25,35) | b | 0.20 |
| 第3组 | [35,45) | 6 | 0.20 |
| 第4组 | [45,55) | 12 | 0.60 |
| 第5组 | [55,65] | 20 | 0.40 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{3\sqrt{2}}{4}$ | C. | $\sqrt{2}$ | D. | $\frac{5\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若l∥α,l⊥m,则m⊥α | B. | 若l∥α,l⊥m,m?β,则α⊥β | ||
| C. | 若l∥α,l∥m,则m∥α | D. | 若α∥β,l∥α,l∥m,m?β,则m∥β |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com