练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．已知点A（1，-1），B（2，2），点P在直线y=x上，求|PA|2+|PB|2取得最小值时P点的坐标．

    分析 先设出点P的坐标，设P（t，t），由两点间距离公式表示出|PA|2+|PB|2的关于参数t的表达式，再利用函数的相关知识求解出函数的最小值，即得出|PA|2+|PB|2取得最小值与坐标．

    解答 解：设P（t，t），则|PA|2+|PB|2=（t-1）2+（t+1）2+（t-2）2+（t-2）2=4t2-8t+10，
    当t=1时，|PA|2+|PB|2取得最小值，此时有P（1，6），
    所以|PA|2+|PB|2取得最小值时P点的坐标为（1，6）．

    点评 本题考点是两点间距离公式，考查用两点间距离公式建立起相关量的函数关系，转化为求函数的最值，转化思想是数学中的重要思想，由未知向已知转化是解决问题的一个实用的技巧．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    6．关于x的方程x2-（m+2）x+1=0有两个正根，则m的取值范围为{m|m≥0}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．若x＞4，则函数y=x+$\frac{9}{x-4}$（　　）
    A．有最大值10B．有最小值10C．有最大值6D．有最小值6

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

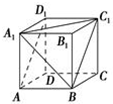    4．如图在正方体ABCDA1B1C1D1中判断下列位置关系：
    （1）AD1所在直线与平面BCC1的位置关系是平行；
    （2）平面A1BC1与平面ABCD的位置关系是相交．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知函数f（x）=log2（ax2+2x+3），若对于任意实数k，总存在实数x0，使得f（x0）=k成立，则实数a的取值范围是（　　）
    A．$[-1，\frac{1}{3}）$B．$[0，\frac{1}{3}]$C．[3，+∞）D．（-1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知命题p：ex＞1，命题q：log2x＜0，则p是q的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知集合B={-1，0，1}，若A⊆B，则满足条件的A有8 个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．设函数f（x）=x2-4|x|+5．
    （1）用分段函数的形式表示该函数并画出该函数的图象；
    （2）写出该函数的值域以及函数的单调递减区间（不用写过程）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．等差数列{an}的前n项和为Sn，a3+a8＜0，S11＞0，当Sn取得最小值时，n=5．

    查看答案和解析>>

    同步练习册答案