
| A. | y=sin2x | B. | y=tan2x | C. | y=sin2x+cos2x | D. | y=sinxcosx |
分析 根据题意,依次分析选项,求出函数的周期与奇偶性,分析即可得答案.
解答 解:根据题意,依次分析选项:
对于A、y=sin2x=$\frac{1-cos2x}{2}$,为偶函数,周期为$\frac{2π}{2}$=π,不符合题意;
对于B、y=tan2x,为奇函数,其周期为$\frac{π}{2}$,不符合题意;
对于C、y=sin2x+cos2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$),为非奇非偶函数,不符合题意;
对于D、y=sinxcosx=$\frac{1}{2}$sin2x,为奇函数,且其周期为$\frac{2π}{2}$=π,符合题意;
故选:D.
点评 本题考查三角函数的周期的计算,关键是正确将三角函数化简变形.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
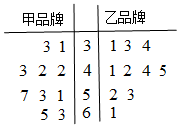 某商场对甲、乙两种品牌的商品进行为期100天的营销活动,为调查这100天的日销售情况,随机抽取了10天的日销售量(单位:件)作为样本,样本数据的茎叶图如图.若日销量不低于50件,则称当日为“畅销日”.
某商场对甲、乙两种品牌的商品进行为期100天的营销活动,为调查这100天的日销售情况,随机抽取了10天的日销售量(单位:件)作为样本,样本数据的茎叶图如图.若日销量不低于50件,则称当日为“畅销日”.| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
| 畅销日天数 | 非畅销日天数 | 合计 | |
| 甲品牌 | 50 | 50 | 100 |
| 乙品牌 | 30 | 70 | 100 |
| 合计 | 80 | 120 | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com