
分析 利用有理数指数幂的性质、运算法则求解.
解答 解:${({2\frac{7}{9}})^{0.5}}+{0.1^{-2}}+{({2\frac{10}{27}})^{-\frac{2}{3}}}-{π^0}+\frac{37}{48}$
=($\frac{25}{9}$)${\;}^{\frac{1}{2}}$+(10-1)-2+[($\frac{4}{3}$)3]${\;}^{-\frac{2}{3}}$-1+$\frac{37}{48}$
=$\frac{5}{3}+100$-$\frac{9}{16}$-1+$\frac{37}{48}$
=$\frac{807}{8}$.
故答案为:$\frac{807}{8}$.
点评 本题考查有理数指数幂化简求值,是基础题,解题时要认真审题,注意有理数指数幂的性质、运算法则的合理运用.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:选择题
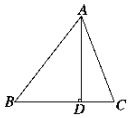 如图所示,在△ABC中,AD⊥BC于D,下列条件:
如图所示,在△ABC中,AD⊥BC于D,下列条件:| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>0,b2+3ac≥0 | B. | a>0,b2-3ac≤0 | C. | a<0,b2+3ac≥0 | D. | a<0,b2-3ac≤0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com