
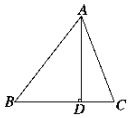
 如图所示,在△ABC中,AD⊥BC于D,下列条件:
如图所示,在△ABC中,AD⊥BC于D,下列条件:| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
分析 根据已知对各个条件进行分析,从而得到答案.
解答 解:(1)不能,∵AD⊥BC,∴∠B+∠BAD=90°,∵∠B+∠DAC=90°,∴∠BAD=∠DAC,∴无法证明△ABC是直角三角形;
(2)能,∵∠B=∠DAC,则∠BAD=∠C,∴∠B+∠BAD=∠C+∠DAC=180°÷2=90°;
(3)能
∵CD:AD=AC:AB,∠ADB=∠ADC=90°,
∴Rt△ABD∽Rt△CAD(直角三角形相似的判定定理),
∴∠ABD=∠CAD;∠BAD=∠ACD
∵∠ABD+∠BAD=90°
∴∠CAD+∠BAD=90°
∵∠BAC=∠CAD+∠BAD
∴∠BAC=90°;
(4)能,∵能说明△CBA∽△ABD,∴△ABC一定是直角三角形.
共有3个.
故选A.
点评 通过计算角相等和边成比例,判断出两个三角形是否相似,进而判断出是否为直角.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,-$\frac{1}{5}$) | B. | ($\frac{1}{5}$,1) | C. | (-∞,-1)∪(-$\frac{1}{5}$,+∞) | D. | (-∞,-5)∪(-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com