
���� Ӫ��ѧ��ָ��������ѧ�����õ��ճ���ʳӦ�������ṩ0.075kg��̼ˮ�����0.06kg�ĵ����ʣ�0.06kg��֬����1kgʳ��A����0.105kg̼ˮ�����0.07kg�����ʣ�0.14kg֬��������35Ԫ����1kgʳ��B����0.105kg̼ˮ�����0.14kg�����ʣ�0.07kg֬��������28Ԫ��Ϊ������Ӫ��ר��ָ���� �ճ���ʳҪ��ͬʱʹ������ͣ���Ҫͬʱʳ��ʳ��A��ʳ��B����kg��
��ÿ��ʳ��xkgAʳ�ykgBʳ��ܳɱ�Ϊz������Լ���������������Թ滮��֪ʶ������⣮
���  �⣺��ÿ��ʳ��xkgAʳ�ykgBʳ��ܳɱ�Ϊz����$\left\{\begin{array}{l}{0.105x+0.105y��0.075}\\{0.07x+0.14y��0.06}\\{0.14x+0.07y��0.06}\\{y��0}\\{x��0}\end{array}\right.$Ŀ�꺯��Ϊz=28x+21y------------------4��
�⣺��ÿ��ʳ��xkgAʳ�ykgBʳ��ܳɱ�Ϊz����$\left\{\begin{array}{l}{0.105x+0.105y��0.075}\\{0.07x+0.14y��0.06}\\{0.14x+0.07y��0.06}\\{y��0}\\{x��0}\end{array}\right.$Ŀ�꺯��Ϊz=28x+21y------------------4��
����ʽ�黯��Ϊ$\left\{\begin{array}{l}{7x+7y��5}\\{7x+14y��6}\\{14x+7y��6}\\{y��0}\\{x��0}\end{array}\right.$��ͼ������������Ӱ���֣���---------------------------------------6��
��z=28x+21y����Ϊy=-$\frac{4}{3}$x+$\frac{z}{21}$��
��ͼ�ɼ�����ֱ��z=28x+21y�����������ϵĵ�Mʱz��С��-------8��
�ⷽ����$\left\{\begin{array}{l}{7x+7y=5}\\{14x+7y=6}\end{array}\right.$��M������Ϊ��$\frac{1}{7}$��$\frac{4}{7}$��--------------10��
����zmin=28x+21y=16
��ÿ��ʳ��AԼ143g��ʳ��BԼ571g���ܹ������ճ���ʳҪ����ʹ������ͣ���ͳɱ�16Ԫ��
�ʴ�Ϊ��16����--------------12�֣�
���� ������Ҫ�������Թ滮��Ӧ�ã�����Լ���������������ν���ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
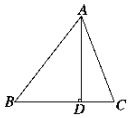 ��ͼ��ʾ���ڡ�ABC�У�AD��BC��D������������
��ͼ��ʾ���ڡ�ABC�У�AD��BC��D������������| A�� | 3�� | B�� | 2�� | C�� | 1�� | D�� | 0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2��-1 | B�� | $\frac{{-1��\sqrt{5}}}{2}$ | C�� | $\frac{{1��\sqrt{5}}}{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | 5 | C�� | 4 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3-4i | B�� | 3+4i | C�� | 4-3i | D�� | 4+3i |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com