
分析 (1)由sinα是方程5x2-7x-6=0的根,解得sinα=-$\frac{3}{5}$,再求出$ta{n}^{2}α=\frac{9}{16}$,利用三角函数的诱导公式即可得出$\frac{cos(2π-α)cos(π+α)ta{n}^{2}(2π-α)}{cos(\frac{π}{2}+α)sin(2π-α)co{t}^{2}(π-α)}$的值.
(2)由sinA+cosA=$\frac{\sqrt{2}}{2}$,①求出2sinAcosA=-$\frac{1}{2}$,再由角的范围求出sinA-cosA=$\frac{\sqrt{6}}{2}$.②,联立①②即可解得sinA,cosA的值,则tanA的值可求.
解答 解:(1)由sinα是方程5x2-7x-6=0的根,解得sinα=-$\frac{3}{5}$,或sinα=2(舍去),
∴$ta{n}^{2}α=\frac{si{n}^{2}α}{co{s}^{2}α}=\frac{(-\frac{3}{5})^{2}}{1-(-\frac{3}{5})^{2}}=\frac{9}{16}$.
$\frac{cos(2π-α)cos(π+α)ta{n}^{2}(2π-α)}{cos(\frac{π}{2}+α)sin(2π-α)co{t}^{2}(π-α)}$=$\frac{cosα(-cosα)(-tanα)^{2}}{(-sinα)(-sinα)(-cotα)^{2}}$
=$-\frac{co{s}^{2}αta{n}^{2}α}{si{n}^{2}αco{t}^{2}α}$=-tan2α=$-\frac{9}{16}$.
(2)∵sinA+cosA=$\frac{\sqrt{2}}{2}$,①
∴(sinA+cosA)2=$\frac{1}{2}$,即1+2sinAcosA=$\frac{1}{2}$,
∴2sinAcosA=-$\frac{1}{2}$.
∵0°<A<180°,∴sinA>0,cosA<0.sinA-cosA>0.
∵(sinA-cosA)2=1-2sinAcosA=$\frac{3}{2}$,
∴sinA-cosA=$\frac{\sqrt{6}}{2}$.②
①+②,得sinA=$\frac{\sqrt{2}+\sqrt{6}}{4}$.①-②,得cosA=$\frac{\sqrt{2}-\sqrt{6}}{4}$.
∴tanA=$\frac{sinA}{cosA}$=$\frac{\sqrt{2}+\sqrt{6}}{4}$×$\frac{4}{\sqrt{2}-\sqrt{6}}$=-2-$\sqrt{3}$.
点评 本题考查了一元二次方程的解法、三角函数求值、三角函数基本关系式、诱导公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
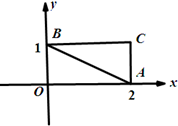 已知椭圆C的方程为$\frac{x^2}{{4{m^2}}}+\frac{y^2}{m^2}$=1,(m>0),如图,△ABC的三个顶点的坐标分别为A(2,0),B(0,1),C(2,1).
已知椭圆C的方程为$\frac{x^2}{{4{m^2}}}+\frac{y^2}{m^2}$=1,(m>0),如图,△ABC的三个顶点的坐标分别为A(2,0),B(0,1),C(2,1).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
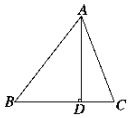 如图所示,在△ABC中,AD⊥BC于D,下列条件:
如图所示,在△ABC中,AD⊥BC于D,下列条件:| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>0,b2+3ac≥0 | B. | a>0,b2-3ac≤0 | C. | a<0,b2+3ac≥0 | D. | a<0,b2-3ac≤0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com