
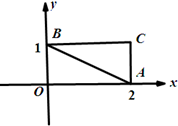
 已知椭圆C的方程为$\frac{x^2}{{4{m^2}}}+\frac{y^2}{m^2}$=1,(m>0),如图,△ABC的三个顶点的坐标分别为A(2,0),B(0,1),C(2,1).
已知椭圆C的方程为$\frac{x^2}{{4{m^2}}}+\frac{y^2}{m^2}$=1,(m>0),如图,△ABC的三个顶点的坐标分别为A(2,0),B(0,1),C(2,1).分析 (Ⅰ)由椭圆焦点在x轴上,则a2=4m2,b2=m2,根据离心率公式即可求得椭圆C的离心率;
(Ⅱ) 当椭圆C在直线AB的左下方时,设直线l方程,代入椭圆方程,由△<0,即可求得m的取值范围,当△ABC在椭圆内时,当且仅当点C(2,1)在椭圆内,将C代入椭圆方程,即可求得m的取值范围;
(Ⅲ)由(Ⅱ)知当$\frac{{\sqrt{2}}}{2}<m<\sqrt{2}$时,当$\frac{{\sqrt{2}}}{2}<m≤1$时,求得丨MN丨,根据三角形的面积公式,即可求得m的值,当$1<m<\sqrt{2}$时,求得M和N的坐标,S=S矩形OACB-S△OBM-S△OAN-S△MNC=2-m2,则${m^2}=2-\frac{{\sqrt{2}}}{4}$,即可求得椭圆的方程/
解答 解 (Ⅰ) 由已知可得,a2=4m2,b2=m2,
椭圆的离心率$e=\frac{c}{a}=\sqrt{\frac{c^2}{a^2}}=\sqrt{\frac{{{a^2}-{b^2}}}{a^2}}=\sqrt{\frac{{3{m^2}}}{{4{m^2}}}}=\frac{{\sqrt{3}}}{2}$,
即椭圆C的离心率为$\frac{{\sqrt{3}}}{2}$;--------------------(5分)
(Ⅱ) 由图可知当椭圆C在直线AB的左下方或△ABC在椭圆内时,两者便无公共点(5分)
①当椭圆C在直线AB的左下方时,
将AB:x+2y-2=0即x=2-2y代入方程$\frac{x^2}{{4{m^2}}}+\frac{y^2}{m^2}=1$,
整理得8y2-8y+4-4m2=0,
由△<0,即64-32(4-4m2)=0<0,解得$0<m<\frac{{\sqrt{2}}}{2}$,
∴由椭圆的几何性质可知当$0<m<\frac{{\sqrt{2}}}{2}$时,椭圆C在直线AB的左下方,
②当△ABC在椭圆内时,当且仅当点C(2,1)在椭圆内,
∴可得$\frac{4}{{4{m^2}}}+\frac{1}{m^2}<1$,
又因为m>0,∴$m>\sqrt{2}$,
综上所述,当$0<m<\frac{{\sqrt{2}}}{2}$或$m>\sqrt{2}$时,椭圆C与△ABC无公共点-;-------------------(10分)
(Ⅲ) 由(Ⅱ)知当$\frac{{\sqrt{2}}}{2}<m<\sqrt{2}$时,椭圆C与△ABC相交于不同的两个点M﹑N,
∴①当$\frac{{\sqrt{2}}}{2}<m≤1$时,M﹑N在线段AB上,设M(x1,y1),N(x2,y2),
$|MN|=\sqrt{5}\sqrt{2{m^2}-1}$.△OMN的面积$s=\sqrt{2{m^2}-1}$,得${m^2}=\frac{9}{16}$,
此时椭圆C的方程为$\frac{{4{x^2}}}{9}+\frac{{16{y^2}}}{9}=1$;
②当$1<m<\sqrt{2}$时,点M﹑N分别在线段BC,AC上,易得$M(2\sqrt{{m^2}-1},1)$,$N(2,\sqrt{{m^2}-1})$,
∴S=S矩形OACB-S△OBM-S△OAN-S△MNC=2-$\sqrt{{m}^{2}-1}$-$\sqrt{{m}^{2}-1}$-$\frac{1}{2}$(2-2$\sqrt{{m}^{2}-1}$)(1-$\sqrt{{m}^{2}-1}$),
=2-2$\sqrt{{m}^{2}-1}$-(1-$\sqrt{{m}^{2}-1}$)2=2-m2,
得${m^2}=2-\frac{{\sqrt{2}}}{4}$,此时椭圆C的方程为$\frac{x^2}{{8-\sqrt{2}}}+\frac{{4{y^2}}}{{8-\sqrt{2}}}=1$,
综上,椭圆C的方程为$\frac{{4{x^2}}}{9}+\frac{{16{y^2}}}{9}=1$或$\frac{x^2}{{8-\sqrt{2}}}+\frac{{4{y^2}}}{{8-\sqrt{2}}}=1$.--------------------(15分)
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查三角形的面积公式,考查计算能力,属于中档题.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 休假次数 | 0 | 1 | 2 | 3 |
| 人数 | 1 | 2 | 4 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,-$\frac{1}{5}$) | B. | ($\frac{1}{5}$,1) | C. | (-∞,-1)∪(-$\frac{1}{5}$,+∞) | D. | (-∞,-5)∪(-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com