练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．某单位实行休年假制度三年以来，10名职工休年假的次数进行的调查统计结果如表所示：
    休假次数0123
    人数1243
    根据上表信息解答以下问题：
    （1）从该单位任选两名职工，用η表示这两人休年假次数之和，记“函数f（x）=x2-ηx-1在区间（4，6）上有且只有一个零点”为事件A，求事件A发生的概率P；
    （2）从该单位任选两名职工，用ξ表示这两人休年假次数之差的绝对值，求随机变量ξ的分布列及数学期望Eξ．

    分析 （1）函数f（x）=x2-ηx-1过（0，-1）点，在区间（4，6）上有且只有一个零点，推出η=4或η=5，然后求解概率即可．　　　　　　　　　　　　　　　　　
    （2）从该单位任选两名职工，用ξ表示这两人休年假次数之差的绝对值，则ξ的可能取值分别是0，1，2，3，求出概率，得到ξ的分布列，然后求解期望即可．

    解答 解：（1）函数f（x）=x2-ηx-1过（0，-1）点，在区间（4，6）上有且只有一个零点，
    则必有$\left\{\begin{array}{l}{f（4）＜0}\\{f（6）＞0}\end{array}\right.$即：$\left\{\begin{array}{l}{16-4η-1＜0}\\{36-6η-1＞0}\end{array}\right.$，解得：$\frac{15}{4}＜η＜\frac{35}{6}$
    所以，η=4或η=5　　　　　　　　　　　　　　　　　　　　…（3分）
    当η=4时，P1=$\frac{{C}_{4}^{2}+{C}_{2}^{1}{C}_{3}^{1}}{{C}_{10}^{2}}$=$\frac{4}{15}$，当η=5时，${P_2}=\frac{C_4^1C_3^1}{{C_{10}^2}}=\frac{4}{15}$
    η=4与η=5为互斥事件，由互斥事件有一个发生的概率公式
    所以　$P={P_1}+{P_2}=\frac{4}{15}+\frac{4}{15}=\frac{8}{15}$…（6分）
    （2）从该单位任选两名职工，用ξ表示这两人休年假次数之差的绝对值，
    则ξ的可能取值分别是0，1，2，3，…（7分）
    于是$P（{ξ=0}）=\frac{C_2^2+C_4^2+C_3^2}{{C_{10}^2}}=\frac{2}{9}$，$P（{ξ=1}）=\frac{C_2^1+C_2^1C_4^1+C_4^1C_3^1}{{C_{10}^2}}=\frac{22}{45}$，
    $P（{ξ=2}）=\frac{C_4^1+C_2^1C_3^1}{{C_{10}^2}}=\frac{2}{9}$，P（ξ=3）=$\frac{{C}_{3}^{1}}{{C}_{10}^{2}}$=$\frac{1}{15}$　　…（10分）
    从而ξ的分布列：

    ξ0123
    P$\frac{2}{9}$$\frac{22}{45}$$\frac{2}{9}$$\frac{1}{15}$
    ξ的数学期望：$Eξ=0×\frac{2}{9}+1×\frac{22}{45}+2×\frac{2}{9}+3×\frac{1}{15}=\frac{17}{15}$．   　…12

    点评 本题考查离散性随机变量的分布列的期望的求法，函数的零点判判断定理的应用，考查转化思想以及计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    14．已知函数$f（x）={log_a}\frac{x-2}{x+2}$的定义域为[m，n]，值域为[logaa（n-1），logaa（m-1）]，且f（x）在[m，n]上为减函数．（常数a＞0，且a≠1）
    （1）求证m＞2
    （2）求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．对于a＞0，a≠1，下列结论中
    （1）am+an=am+n
    （2）${（{a^m}）^n}={a^{m^n}}$
    （3）若M=N，则logaM=logaN
    （4）若${log_a}{M^2}={log_a}{N^2}$，
    则M=N正确的结论有（　　）
    A．3个B．2个C．1个D．0个

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．类比平面内“垂直于同一条直线的两条直线互相平行”的性质，可推出空间下列结论，则其中正确的结论的个数有（　　）
    ①垂直于同一条直线的两条直线互相平行
    ②垂直于同一个平面的两条直线互相平行
    ③垂直于同一条直线的两个平面互相平行
    ④垂直于同一个平面的两个平面互相平行．
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．甲、乙两人各进行一次射击，如果两人击中目标的概率是0.8．计算，至少有1人击中目标的概率0.96．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知椭圆$E：\frac{x^2}{5}+\frac{y^2}{4}=1$的右焦点为F，设直线l：x=5与x轴的交点为E，过点F且斜率为k的直线l1与椭圆交于A，B两点，M为线段EF的中点．
    （I）若直线l1的倾斜角为$\frac{π}{4}$，求△ABM的面积S的值；
    （Ⅱ）过点B作直线BN⊥l于点N，证明：A，M，N三点共线．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．设公差不为零的等差数列{an}的前n项和为Sn，若a5=5a3，则$\frac{{S}_{9}}{{S}_{5}}$=9．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

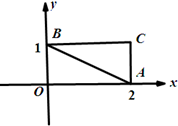    1．已知椭圆C的方程为$\frac{x^2}{{4{m^2}}}+\frac{y^2}{m^2}$=1，（m＞0），如图，△ABC的三个顶点的坐标分别为A（2，0），B（0，1），C（2，1）．
    （Ⅰ） 求椭圆C的离心率；
    （Ⅱ） 若椭圆C与△ABC无公共点，求m的取值范围；
    （Ⅲ） 若椭圆C与△ABC相交于不同的两个点分别为M，N．若△OMN的面积为$\frac{{\sqrt{2}}}{4}$（O为坐标原点），求椭圆C的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知a，b，c均为正数．
    （1）若a+b=1，求$\frac{1}{a}+\frac{4}{b}$的最小值；
    （2）若a+b+c=m，求证：$\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}$≥m．

    查看答案和解析>>

    同步练习册答案