
【题目】已知函数![]()
![]() 且
且![]() 是奇函数.
是奇函数.
(1)求实数![]() 的值;
的值;
(2)若![]() ,对任意
,对任意![]() 都有
都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设![]()
![]() 且
且![]() ,若
,若![]() ,是否存在实数
,是否存在实数![]() 使函数
使函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】
(1)由奇函数的性质![]() ,可求出
,可求出![]() 的值;(2)由
的值;(2)由![]() ,可以求出
,可以求出![]() 的范围,进而可以得到
的范围,进而可以得到![]() 的单调性,然后利用
的单调性,然后利用![]() 奇函数的性质,可以得到
奇函数的性质,可以得到![]() ,从而得到对任意
,从而得到对任意![]() 都有
都有![]() 恒成立,利用二次函数的性质即可求出
恒成立,利用二次函数的性质即可求出![]() 的取值范围;(3)由
的取值范围;(3)由![]() 可求出
可求出![]() ,假设存在实数
,假设存在实数![]() ,构造函数
,构造函数![]() ,则
,则![]() ,对
,对![]() 进行分类讨论,即可判断
进行分类讨论,即可判断![]() 的值。
的值。
(1)因为![]() 的定义域为
的定义域为![]() ,且
,且![]() 为奇函数,
为奇函数,
所以![]() ,解得
,解得![]() .检验:当
.检验:当![]() 时,
时,![]() ,
,
对任意![]() ,都有
,都有![]() ,即
,即![]() 是奇函数,所以
是奇函数,所以![]() 成立。
成立。
(2)由(1)可得![]() ,由
,由![]() 可得
可得![]()
因为![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
则![]() 在
在![]() 单调递减,
单调递减,![]() 在
在![]() 单调递增,
单调递增,
所以![]() 在
在![]() 单调递减,
单调递减,
由![]() 可得
可得![]() ,
,
所以对任意![]() 都有
都有![]() 恒成立,
恒成立,
即![]() 对任意
对任意![]() 恒成立,
恒成立,
所以![]() ,解得
,解得![]() .
.
(3)![]() ,
,
由![]() 可得
可得![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() .
.
所以![]() ,易知
,易知![]() 在
在![]() 单调递增.
单调递增.
令![]() ,则
,则![]() ,
,
再令![]() ,则
,则![]()
因为![]() ,
,![]() ,
,
![]() ,
,
所以![]() .因为
.因为![]() 在
在![]() 有意义,
有意义,
所以对任意![]() ,都有
,都有![]() 恒成立,
恒成立,
所以![]() ,即
,即![]()
所以![]() ,所以
,所以![]() .
.
二次函数![]() 图像开口向上,对称轴为直线
图像开口向上,对称轴为直线![]() ,
,
因为![]() ,所以
,所以![]() ,
,
对称轴始终在区间![]() 的左侧
的左侧
所以![]() 在区间
在区间![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,
![]() 时,
时,![]() ,
,
假设存在满足条件的实数![]() ,则:
,则:
若![]() ,则
,则![]() 为减函数,
为减函数,![]() ,
,
即![]() ,所以
,所以![]() ,舍去;
,舍去;
若![]() ,则
,则![]() 为增函数,
为增函数,![]() ,
,
即![]() ,所以
,所以![]() ,舍去.
,舍去.
综上所述,不存在满足条件的实数![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,分别过椭圆![]() 左、右焦点
左、右焦点![]() 的动直线
的动直线![]() 相交于
相交于![]() 点,与椭圆
点,与椭圆![]() 分别交于
分别交于![]() 与
与![]() 不同四点,直线
不同四点,直线![]() 的斜率
的斜率![]() 满足
满足![]() .已知当
.已知当![]() 与
与![]() 轴重合时,
轴重合时,![]() ,
,![]() .
.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求出
为定值?若存在,求出![]() 点坐标并求出此定值;若不存在,说明理由.
点坐标并求出此定值;若不存在,说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ,
,![]() 和
和![]() .
.
【解析】试题分析:(1)当![]() 与
与![]() 轴重合时,
轴重合时,![]() 垂直于
垂直于![]() 轴,得
轴,得![]() ,得
,得![]() ,
,![]() 从而得椭圆的方程;(2)由题目分析如果存两定点,则
从而得椭圆的方程;(2)由题目分析如果存两定点,则![]() 点的轨迹是椭圆或者双曲线 ,所以把
点的轨迹是椭圆或者双曲线 ,所以把![]() 坐标化,可得
坐标化,可得![]() 点的轨迹是椭圆,从而求得定点
点的轨迹是椭圆,从而求得定点![]() 和点
和点![]() .
.
试题解析:![]() 当
当![]() 与
与![]() 轴重合时,
轴重合时,![]() , 即
, 即![]() ,所以
,所以![]() 垂直于
垂直于![]() 轴,得
轴,得![]() ,
,![]() ,, 得
,, 得![]() ,
,![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
![]() 焦点
焦点![]() 坐标分别为
坐标分别为![]() , 当直线
, 当直线![]() 或
或![]() 斜率不存在时,
斜率不存在时,![]() 点坐标为
点坐标为![]() 或
或![]() ;
;
当直线![]()
![]() 斜率存在时,设斜率分别为
斜率存在时,设斜率分别为![]() , 设
, 设![]()
![]() 由
由 , 得:
, 得:
![]() , 所以:
, 所以:![]() ,
,![]() , 则:
, 则:
![]()
![]() . 同理:
. 同理:![]()
![]() , 因为
, 因为
![]() , 所以
, 所以![]()
![]() , 即
, 即![]() , 由题意知
, 由题意知![]() , 所以
, 所以
![]() , 设
, 设![]() ,则
,则![]() ,即
,即![]() ,由当直线
,由当直线![]() 或
或![]() 斜率不存在时,
斜率不存在时,![]() 点坐标为
点坐标为![]() 或
或![]() 也满足此方程,所以点
也满足此方程,所以点![]() 在椭圆
在椭圆![]() 上.存在点
上.存在点![]() 和点
和点![]() ,使得
,使得![]() 为定值,定值为
为定值,定值为![]() .
.
考点:圆锥曲线的定义,性质,方程.
【方法点晴】本题是对圆锥曲线的综合应用进行考查,第一问通过两个特殊位置,得到基本量![]() ,
,![]() ,得
,得![]() ,
,![]() ,从而得椭圆的方程,第二问由题目分析如果存两定点,则
,从而得椭圆的方程,第二问由题目分析如果存两定点,则![]() 点的轨迹是椭圆或者双曲线 ,本题的关键是从这个角度出发,把
点的轨迹是椭圆或者双曲线 ,本题的关键是从这个角度出发,把![]() 坐标化,求得
坐标化,求得![]() 点的轨迹方程是椭圆
点的轨迹方程是椭圆![]() ,从而求得存在两定点
,从而求得存在两定点![]() 和点
和点![]() .
.
【题型】解答题
【结束】
21
【题目】已知![]() ,
,![]() ,
,![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的极值;
的极值;
(Ⅱ)若函数![]() 的两个零点为
的两个零点为![]() ,记
,记![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量(百件)与销售单价x(元/件)之间的关系用下图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.

(1)把y表示为x的函数;
(2)当销售价为每件50元时,该店正好收支平衡(即利润为零),求该店的职工人数;
(3)若该店只有20名职工,问销售单价定为多少元时,该专卖店可获得最大月利润?(注:利润=收入-支出)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是奇函数,
是奇函数,![]() 为偶函数,
为偶函数,![]() 且(e是自然对数的底数).
且(e是自然对数的底数).
(1)分别求出![]() 和
和![]() 的解析式;
的解析式;
(2)记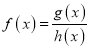 ,请判断
,请判断![]() 的奇偶性和单调性,并分别说明理由;
的奇偶性和单调性,并分别说明理由;
(3)若存在![]() ,使得不等式
,使得不等式![]() 能成立,求实数m的取值范围.
能成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解学生一次考试后数学、物理两个科目的成绩情况,从中随机抽取了25位考生的成绩进行统计分析.25位考生的数学成绩已经统计在茎叶图中,物理成绩如下:

(Ⅰ)请根据数据在答题卡的茎叶图中完成物理成绩统计;

(Ⅱ)请根据数据在答题卡上完成数学成绩的频数分布表及数学成绩的频率分布直方图;
数学成绩分组 | [50,60﹚ | [60,70﹚ | [70,80﹚ | [80,90﹚ | [90,100﹚ | [100,110﹚ | [110,120] |
频数 |

(Ⅲ)设上述样本中第i位考生的数学、物理成绩分别为xi,yi(i=1,2,3,…,25).通过对样本数据进行初步处理发现:数学、物理成绩具有线性相关关系,得到:![]() =86,
=86,![]() =64,
=64,![]() (xi-
(xi-![]() )(yi-
)(yi-![]() )=4698,
)=4698,![]() (xi-
(xi-![]() )2=5524,
)2=5524,![]() ≈0.85.求y关于x的线性回归方程,并据此预测当某考生的数学成绩为100分时,该考生的物理成绩(精确到1分).
≈0.85.求y关于x的线性回归方程,并据此预测当某考生的数学成绩为100分时,该考生的物理成绩(精确到1分).
附:回归直线方程的斜率和截距的最小二乘估计公式分别为:![]() =
= ,
,![]() =
=![]() -
-![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学数学学院拟从往年的智慧队和理想队中选拔4名大学生组成志愿者招募宣传队.往年的智慧对和理想队的构成数据如下表所示,现要求选出的4名大学生中两队中的大学生都要有.

(1)求选出的4名大学生仅有1名女生的概率;
(2)记选出的4名大学生中女生的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了解本市![]() 万名学生的汉字书写水平,在全市范围内进行了汉字听写考试,发现其成绩服从正态分布
万名学生的汉字书写水平,在全市范围内进行了汉字听写考试,发现其成绩服从正态分布![]() ,现从某校随机抽取了
,现从某校随机抽取了![]() 名学生,将所得成绩整理后,绘制出如图所示的频率分布直方图.
名学生,将所得成绩整理后,绘制出如图所示的频率分布直方图.

(1)估算该校![]() 名学生成绩的平均值
名学生成绩的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)求这![]() 名学生成绩在
名学生成绩在![]() 内的人数;
内的人数;
(3)现从该校![]() 名考生成绩在
名考生成绩在![]() 的学生中随机抽取两人,该两人成绩排名(从高到低)在全市前
的学生中随机抽取两人,该两人成绩排名(从高到低)在全市前![]() 名的人数记为
名的人数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:若![]() ,则
,则![]() ,
, ![]()
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com