
【题目】已知抛物线C:y2=2px的焦点为F,过点F且斜率为1的直线l截得圆:x2+y2=p2的弦长为2![]() .
.
(1)求抛物线C的方程;
(2)若过点F作互相垂直的两条直线l1、l2,l1与抛物线C交于A、B两点,l2与抛物线C交于D、E两点,M、N分别为弦AB、DE的中点,求|MF||NF|的最小值.
【答案】(1)y2=8x(2)32
【解析】
(1)求得抛物线C的焦点,可得直线l的方程,求得圆心(0,0)到直线的距离,由圆内的垂径定理,结合勾股定理,解方程可得p,进而得到抛物线的方程;
(2)求得焦点F的坐标,由已知可得AB⊥DE,两直线AB、DE的斜率都存在且均不为0.设直线AB的斜率为k,则直线CD的斜率为![]() ,故直线AB的方程为y=k(x﹣2).联立抛物线的方程,运用韦达定理和中点坐标公式,求得M的坐标,同理可得N的坐标,再由两点的距离公式,结合基本不等式可得所求最小值.
,故直线AB的方程为y=k(x﹣2).联立抛物线的方程,运用韦达定理和中点坐标公式,求得M的坐标,同理可得N的坐标,再由两点的距离公式,结合基本不等式可得所求最小值.
(1)由y2=2px的焦点为F(![]() ,0),
,0),
可得直线l的方程为l:y=x![]() ,
,
圆心到直线l的距离为d![]() ,
,
又d2+14=p2,可得p=4,
故抛物线C的方程为y2=8x;
(2)由(1)知焦点为F(2,0).
由已知可得AB⊥DE,所以两直线AB、DE的斜率都存在且均不为0.
设直线AB的斜率为k,则直线CD的斜率为![]() ,
,
故直线AB的方程为y=k(x﹣2).
联立方程组 ,消去x,整理得ky2﹣8y﹣16k=0,
,消去x,整理得ky2﹣8y﹣16k=0,
设点A(x1,y1),B(x2,y2),则y1+y2![]() .
.
因为M(xM,yM)为弦AB的中点,所以yM![]() (y1+y2)
(y1+y2)![]() .
.
由yM=k(xM﹣2),得xM![]() 2
2![]() 2,故点M(
2,故点M(![]() 2,
2,![]() ),
),
同理,可得N(4k2+2,﹣4k),
故|NF|![]() 4
4![]() ,
,
|MF|![]() .
.
所以|MF||NF|![]() 4
4![]() 16
16![]() 16(|k|
16(|k|![]() )
)
≥16×2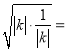 32,
32,
当且仅当|k|![]() ,即k=±1时,等号成立.
,即k=±1时,等号成立.
所以|MF||NF|的最小值为32.


 核心素养学练评系列答案
核心素养学练评系列答案科目:高中数学 来源: 题型:
【题目】某科研团队对![]() 例新冠肺炎确诊患者的临床特征进行了回顾性分析.其中
例新冠肺炎确诊患者的临床特征进行了回顾性分析.其中![]() 名吸烟患者中,重症人数为
名吸烟患者中,重症人数为![]() 人,重症比例约为
人,重症比例约为![]() ;
;![]() 名非吸烟患者中,重症人数为
名非吸烟患者中,重症人数为![]() 人,重症比例为
人,重症比例为![]() .根据以上数据绘制
.根据以上数据绘制![]() 列联表,如下:
列联表,如下:
吸烟人数 | 非吸烟人数 | 总计 | |
重症人数 | 30 | 120 | 150 |
轻症人数 | 100 | 800 | 900 |
总计 | 130 | 920 | 1050 |
(1)根据列联表数据,能否在犯错误的概率不超过![]() 的前提下认为新冠肺炎重症和吸烟有关?
的前提下认为新冠肺炎重症和吸烟有关?
(2)已知每例重症患者平均治疗费用约为![]() 万元,每例轻症患者平均治疗费用约为
万元,每例轻症患者平均治疗费用约为![]() 万元.现有吸烟确诊患者20人,记这
万元.现有吸烟确诊患者20人,记这![]() 名患者的治疗费用总和为
名患者的治疗费用总和为![]() ,求
,求![]() .
.
附:
|
|
|
|
|
|
|
|
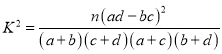
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了有效地加强高中生自主管理能力,推出了一系列措施,其中自习课时间的自主管理作为重点项目,学校有关处室制定了“高中生自习课时间自主管理方案”.现准备对该“方案”进行调查,并根据调查结果决定是否启用该“方案”,调查人员分别在各个年级随机抽取若干学生对该“方案”进行评分,并将评分分成![]() ,
,![]() ,
,![]() ,
,![]() 七组,绘制成如图所示的频率分布直方图.
七组,绘制成如图所示的频率分布直方图.
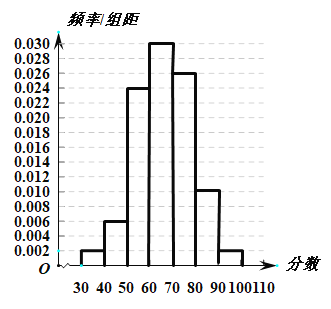
相关规则为①采用百分制评分,![]() 内认定为对该“方案”满意,不低于80分认定为对该“方案”非常满意,60分以下认定为对该“方案”不满意;②学生对“方案”的满意率不低于
内认定为对该“方案”满意,不低于80分认定为对该“方案”非常满意,60分以下认定为对该“方案”不满意;②学生对“方案”的满意率不低于![]() 即可启用该“方案”;③用样本的频率代替概率.
即可启用该“方案”;③用样本的频率代替概率.
(1)从该校学生中随机抽取1人,求被抽取的这位同学非常满意该“方案”的概率,并根据频率分布直方图求学生对该“方案”评分的中位数.
(2)根据所学统计知识,判断该校是否启用该“方案”,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是直角梯形,AB=2CD=2PD=2,PC![]() ,且有PD⊥AD,AD⊥CD,AB∥CD.
,且有PD⊥AD,AD⊥CD,AB∥CD.

(1)证明:PD⊥平面ABCD;
(2)若四棱锥P﹣ABCD的体积为![]() ,求四棱锥P﹣ABCD的表面积.
,求四棱锥P﹣ABCD的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点A是直线
,点A是直线![]() 上的动点,过
上的动点,过![]() 作直线
作直线![]() ,
,![]() ,线段
,线段![]() 的垂直平分线与
的垂直平分线与![]() 交于点
交于点![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若点![]() ,
,![]() 是直线
是直线![]() 上两个不同的点,且
上两个不同的点,且![]() 的内切圆方程为
的内切圆方程为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
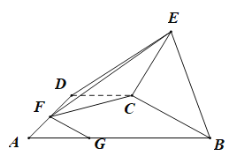
【题目】如图,在直角梯形![]() 中,
中,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 分别在线段
分别在线段![]() 和
和![]() 上,且
上,且![]() ,
,![]() 是等腰直角三角形.
是等腰直角三角形.
(1)若![]() ,求证:
,求证:![]() 平面
平面![]() .
.
(2)![]() ,是否存在
,是否存在![]() ,使得
,使得![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据相关数据统计,2019年底全国已开通![]() 基站13万个,部分省市的政府工作报告将“推进
基站13万个,部分省市的政府工作报告将“推进![]() 通信网络建设”列入2020年的重点工作,今年一月份全国共建基站3万个.
通信网络建设”列入2020年的重点工作,今年一月份全国共建基站3万个.
(1)如果从2月份起,以后的每个月比上一个月多建设2000个,那么,今年底全国共有基站多少万个.(精确到0.1万个)
(2)如果计划今年新建基站60万个,到2022年底全国至少需要800万个,并且,今后新建的数量每年比上一年以等比递增,问2021年和2022年至少各建多少万个オ能完成计划?(精确到1万个)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com