
分析 构造正四面体S-ABC,取SA中点O,连结BO,CO,则BO⊥SA,CO⊥SO,∠BOC是平面SAB与平面SAC所成二面角的平面角,由此能求出平面SAB与平面SAC所成二面角的余弦值.
解答 解: ∵SA、SB、SC两两所成的角为60°,
∵SA、SB、SC两两所成的角为60°,
∴构造正四面体S-ABC,
取SA中点O,连结BO,CO,
设该正四面体棱长为2,
则BO⊥SA,CO⊥SO,
∴∠BOC是平面SAB与平面SAC所成二面角的平面角,
BO=CO=$\sqrt{4-1}=\sqrt{3}$,BC=2,
∴cos∠BOC=$\frac{B{O}^{2}+C{O}^{2}-B{C}^{2}}{2•BO•CO}$
=$\frac{3+3-4}{2×\sqrt{3}×\sqrt{3}}$=$\frac{1}{3}$.
∴平面SAB与平面SAC所成二面角的余弦值为$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查二面角概念及其求法,化归与转化的思想的应用,考查逻辑推理、运算、空间想象能力,属中档题.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (4,+∞) | C. | (2,4] | D. | [2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 回归分析和独立性检验没有什么区别 | |
| B. | 回归分析是对两个变量准确关系的分析,而独立性检验是分析两个变量之间的不确定关系 | |
| C. | 回归分析研究两个变量之间的相关关系,独立性检验是对两个变量是否具有某种关系的一种检验 | |
| D. | 独立性检验可以100%确定两个变量之间是否具有某种关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
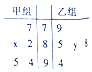 下列茎叶图记录了甲、乙两组各五名学生在一次数学测试中的成绩(单位:分),已知甲组数据的平均数为86,乙组数据的中位数为86,则x,y的值分别为( )
下列茎叶图记录了甲、乙两组各五名学生在一次数学测试中的成绩(单位:分),已知甲组数据的平均数为86,乙组数据的中位数为86,则x,y的值分别为( )| A. | 2,7 | B. | 2,6 | C. | 3,7 | D. | 3,6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com