考点:数量积表示两个向量的夹角,函数单调性的判断与证明,函数的最值及其几何意义
专题:平面向量及应用
分析:(1)首先利用函数的数量积求出向量的夹角.
(2)首先把向量的模长转化为求向量的数量级,进一步利用导数求出单调区间,最后确定最值.
解答:
解:( I ) 依题设:|
|=||
=|
|=1,且
+
=-
⇒(
+
)
2=(-
)
2,化简得:
•
=-
⇒cos<
,
>=-
,又<
,
>∈[0,π]⇒<
,
>=
.
( II )由 ( I )易知:
•
=
•
=
•
=-
,
故由f(x)=|
|=
,
将其展开整理得:f(x)=
(x∈R,x≠0,n∈N
+).①x>0时,对u(x)=x
2+(
)
2-n,求导并整理得:u′(x)=
.
则由u′(x)>0⇒x>
,
且由u′(x)<0⇒0<x<
.即f(x)的增区间为(
,+∞),减区间为(0,
).
②x<0时,因f(x)为偶函数,由图象的对称性知:f(x)的增区间为(-
,0),减区间为(-∞,-
).
综上:f(x)的增区间为 (-
,0)与 (
,+∞),f(x)的减区间为(-∞,-
) 和 (0,
).
再由均值不等式易求得:|x|=
时,f(x)
min=
.
点评:本题考查的知识点:向量的数量积,向量的夹角,向量的模,均值不等式,利用导数求函数的单调区间和最值及相关的运算问题.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案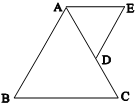 如图所示,等边△ABC的边长为2,D为AC中点,且△ADE也是等边三角形,在△ADE以点A为中心向下转动到稳定位置的过程中,
如图所示,等边△ABC的边长为2,D为AC中点,且△ADE也是等边三角形,在△ADE以点A为中心向下转动到稳定位置的过程中,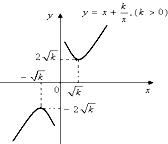 函数f(x)=x+
函数f(x)=x+